题目内容
13. 如图:在△ABC中,AB=AC=$\sqrt{5}$,BC=4,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为1.
如图:在△ABC中,AB=AC=$\sqrt{5}$,BC=4,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为1.
分析 首先根据等腰三角形的性质可得AD⊥BC,再利用勾股定理计算出AD长,然后再证明AD=DF可得答案.
解答 解:∵△ABC是等腰三角形,D为底边的中点,
∴AD⊥BC,
∵BC=4,
∴BD=2,
∵AB=AC=$\sqrt{5}$,
∴AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{5-4}$=1,
∵AE是∠BAD的角平分线,
∴∠DAE=∠EAB,
∵DF∥AB,
∴∠BAF=∠F,
∴∠DAE=∠F,
∴AD=DF=1,
故答案为:1.
点评 此题主要考查了等腰三角形的性质,以及平行线的性质,关键是掌握等腰三角形顶角平分线、底边上的高、底边上的中线三线合一.

练习册系列答案
相关题目
1.下列说法中,错误的是( )
| A. | 一组邻边相等的平行四边形是菱形 | |
| B. | 对角线互相垂直的平行四边形是菱形 | |
| C. | 四条边相等的四边形是菱形 | |
| D. | 对角线相等且互相平分的四边形是菱形 |
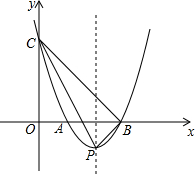 如图所示,已知抛物线与x轴交于A(1,0),B(3,0)两点,与y轴交于点C(0,3),P是抛物线的顶点,连接BC,CP,BP.求:
如图所示,已知抛物线与x轴交于A(1,0),B(3,0)两点,与y轴交于点C(0,3),P是抛物线的顶点,连接BC,CP,BP.求:
 如图,方格纸中的每个小方格都是边长为1个单位的正方形,建立平面直角坐标系后,△ABC的顶点都在格点上,点C的坐标为(0,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,建立平面直角坐标系后,△ABC的顶点都在格点上,点C的坐标为(0,-1).