题目内容
13.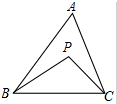 如图,在△ABC中,∠ABP=2∠PBC,∠ACP=2∠PCB.
如图,在△ABC中,∠ABP=2∠PBC,∠ACP=2∠PCB.(1)若∠BPC=140°,求∠A的度数.
(2)求证:∠P=120°+$\frac{1}{3}$∠A.
分析 (1)要求∠A的度数,只需求出∠ABC+∠ACB的度数,只需求出∠PBC+∠PCB,只需运用三角形内角和定理即可解决问题;
(2)根据三角形内角和定理,将∠P转化为∠PBC+∠PCB,结合条件可转化为∠ABC+∠ACB,进而转化为∠A,问题得以解决.
解答 解:(1)∵∠BPC=140°,∴∠PBC+∠PCB=180°-140°=40°.
∵∠ABP=2∠PBC,∠ACP=2∠PCB,
∴∠ABC=3∠PBC,∠ACB=3∠PCB,
∴∠ABC+∠ACB=3(∠PBC+∠PCB)=3×40°=120°,
∴∠A=180°-120°=60°;
(2)∠P=180°-(∠PBC+∠PCB)
=180°-$\frac{1}{3}$(∠ABC+∠ACB)
=180°-$\frac{1}{3}$(180°-∠A)
=120°+$\frac{1}{3}$∠A.
点评 本题主要考查了三角形的内角和定理,运用整体思想是解决本题的关键.

练习册系列答案
相关题目
4.我们规定:将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“等积线”,等积线被这个平面图形截得的线段叫做该图形的“等积线段”(例如三角形的中线就是三角形的等积线段).已知菱形的边长为4,且有一个内角为60°,设它的等积线段长为m,则m的取值范围是( )
| A. | m=4或m=4$\sqrt{3}$ | B. | 4≤m≤4$\sqrt{3}$ | C. | 2$\sqrt{3}≤m≤4\sqrt{3}$ | D. | 2$\sqrt{3}$≤m≤4 |