题目内容
15.已知直线y=2x-b与两坐标轴所围成的三角形面积等于4,直线解析式为y=2x+4或y=2x-4.分析 直线y=2x-b与x轴的交点坐标是($\frac{b}{2}$,0),与y轴的交点坐标是(0,-b),根据三角形的面积是4可得b值,从而求出直线解析式.
解答 解:直线y=2x-b与x轴的交点坐标是($\frac{b}{2}$,0),与y轴的交点坐标是(0,-b),
则$\frac{1}{2}•|\frac{b}{2}|•$|-b|=4,
即$\frac{{b}^{2}}{4}$=4,
解得:b=4或-4,
故直线解析式为:y=2x+4或y=2x-4.
故答案为:y=2x+4或y=2x-4.
点评 本题考查了一次函数图象上点的坐标特征,本题要注意利用三角形的面积,列出方程,求出未知数,从而求出函数的解析式.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
1.下列说法中,错误的是( )
| A. | 一组邻边相等的平行四边形是菱形 | |
| B. | 对角线互相垂直的平行四边形是菱形 | |
| C. | 四条边相等的四边形是菱形 | |
| D. | 对角线相等且互相平分的四边形是菱形 |
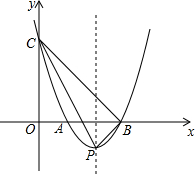 如图所示,已知抛物线与x轴交于A(1,0),B(3,0)两点,与y轴交于点C(0,3),P是抛物线的顶点,连接BC,CP,BP.求:
如图所示,已知抛物线与x轴交于A(1,0),B(3,0)两点,与y轴交于点C(0,3),P是抛物线的顶点,连接BC,CP,BP.求: