题目内容
16.请阅读下面解方程(x2+1)2-2(x2+1)-3=0的过程.解:设x2+1=y,则原方程可变形为y2-2y-3=0.
解得y1=3,y2=-1.
当y=3时,x2+1=3,∴x=±$\sqrt{2}$.
当y=-1时,x2+1=-1,x2=-2此方程无实数解.
∴原方程的解为x1=$\sqrt{2}$,x2=-$\sqrt{2}$.
我们将上述解方程的方法叫做换元法.
请用换元法解方程:($\frac{x}{x-1}$)2-2($\frac{x}{x-1}$)-15=0.
分析 根据材料的提示,可以利用换元法解答分式方程,注意最后要验根.
解答 解:($\frac{x}{x-1}$)2-2($\frac{x}{x-1}$)-15=0,
设$\frac{x}{x-1}$=a,
则a2-2a-15=0,
解得,a=-3或a=5,
当a=-3时,$\frac{x}{x-1}=-3$,解得,x=$\frac{3}{4}$,经检验x=$\frac{3}{4}$是分式方程的解,
当a=5时,$\frac{x}{x-1}=5$,解得x=$\frac{5}{4}$,经检验x=$\frac{5}{4}$是分式方程的解,
∴原分式方程的解是${x}_{1}=\frac{3}{4}$,${x}_{2}=\frac{5}{4}$.
点评 本题考查换元法解一元二次方程、换元法解解分式方程,解题的关键是明确用换元法解方程的方法.

练习册系列答案
相关题目
4.声音在空气中传播的速度y(m/s)与气温x(℃)的关系,如表列出了一组不同气温时的音速.
(1)求出y与x之间的函数关系式(不必写出自变量的取值范围);
(2)当声音在空气中的传播速度为343米/秒,气温多少?
(3)当气温为22℃时,某人看到烟花燃放5秒后才听到声响,那么此人与燃放烟花所在地相距多远?
| 气温x (℃) | … | 0 | 5 | 10 | 15 | … |
| 音速y (m/s) | … | 331 | 334 | 337 | 340 | … |
(2)当声音在空气中的传播速度为343米/秒,气温多少?
(3)当气温为22℃时,某人看到烟花燃放5秒后才听到声响,那么此人与燃放烟花所在地相距多远?
6.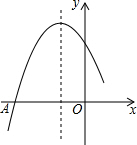 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论,其中正确结论是( )
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论,其中正确结论是( )
 如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论,其中正确结论是( )
如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为直线x=-1,给出四个结论,其中正确结论是( )| A. | b2<4ac | |
| B. | 2a+b=0 | |
| C. | a+b+c>0 | |
| D. | 若点B($\frac{5}{2}$,y1)、C($\frac{1}{2}$,y2)为函数图象上的两点,则y1<y2 |
 如图①,已知△ABC是等腰三角形,∠BAC=90°,点D是BC的中点,作正方形DEFG,使点A、C分别在DG和DE上,连接AE、BG.
如图①,已知△ABC是等腰三角形,∠BAC=90°,点D是BC的中点,作正方形DEFG,使点A、C分别在DG和DE上,连接AE、BG. 如图,已知抛物线l1经过原点与A点,其顶点是P(-2,3),平行于y轴的直线m与x轴交于点B(b,0),与抛物线l1交于点M.
如图,已知抛物线l1经过原点与A点,其顶点是P(-2,3),平行于y轴的直线m与x轴交于点B(b,0),与抛物线l1交于点M.