Question

6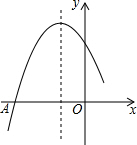．如图是二次函数y=ax²+bx+c图象的一部分，图象过点A（-3，0），对称轴为直线x=-1，给出四个结论，其中正确结论是（　　）

• A． b²＜4ac
• B． 2a+b=0
• C． a+b+c＞0
• D． 若点B（$\frac{5}{2}$，y₁）、C（$\frac{1}{2}$，y₂）为函数图象上的两点，则y₁＜y₂

Answer 1

分析 根据抛物线与x轴交点个数可判断选项A；根据抛物线对称轴可判断选项B；根据抛物线与x轴的另一个交点坐标可判断选项C；根据函数图象的性质可判断选项D．

解答 解：A、∵由函数图象可知抛物线与x轴有2个交点，
∴b²-4ac＞0即b²＞4ac，故本题选项错误；
B、∵对称轴为直线x=-1，
∴-$\frac{b}{2a}$=-1，即2a-b=0，故本选项错误；
C、∵抛物线与x轴的交点A坐标为（-3，0）且对称轴为x=-1，
∴抛物线与x轴的另一交点为（1，0），
∴将（1，0）代入解析式可得，a+b+c=0，故本选项错误；
D、∵抛物线的对称轴是直线x=-1，抛物线的开口向下，
∴当x＞-1时，y随x的增大而减小，
∵-1＜$\frac{1}{2}$＜$\frac{5}{2}$，点B（$\frac{5}{2}$，y₁）、C（$\frac{1}{2}$，y₂）为函数图象上的两点，
∴y₁＜y₂，故本选项正确；
故选D．

点评 本题考查了二次函数图象与系数的关系，二次函数y=ax²+bx+c（a≠0），a的符号由抛物线开口方向决定；b的符号由对称轴的位置及a的符号决定；c的符号由抛物线与y轴交点的位置决定；抛物线与x轴的交点个数，决定了b²-4ac的符号，此外还要注意x=1，-3对应函数值的正负来判断其式子的正确与否．