Question

7．如图①，已知△ABC是等腰三角形，∠BAC=90°，点D是BC的中点，作正方形DEFG，使点A、C分别在DG和DE上，连接AE、BG．
（1）试猜想线段BG和AE的关系为；
（2）如图②，将正方形DEFG绕点D按逆时针方向旋转α（0°＜α≤90°），判断（1）中的结论是否仍然成立，证明你的结论．

Answer 1

分析 （1）由等腰直角三角形的性质及正方形的性质就可以得出△ADE≌△BDG就可以得出结论；
（2）如图2，连接AD，由等腰直角三角形的性质及正方形的性质就可以得出△ADE≌△BDG就可以得出结论．

解答 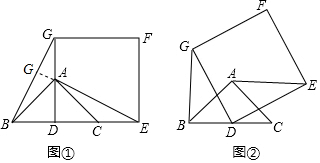解：（1）BG=AE．AE⊥BG，
理由：∵△ABC是等腰直角三角形，∠BAC=90°，点D是BC的中点，
∴AD⊥BC，BD=CD，
∴∠ADB=∠ADC=90°．
∵四边形DEFG是正方形，
∴DE=DG．
在△BDG和△ADE中，
$\left\{\begin{array}{l}{BD=AD}\\{∠BDE=∠ADE}\\{GD=ED}\end{array}\right.$，
∴△ADE≌△BDG（SAS），
∴BG=AE；
∴∠DEA=∠DGB，
∵∠DEA+∠DNE=90°，∠DNE=∠MNG，
∴∠MNG+DGB=90°，
∴AE⊥BG；
（2）成立，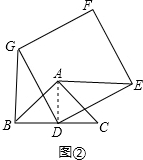
理由：如图②，连接AD，
∵在Rt△BAC中，D为斜边BC中点，
∴AD=BD，AD⊥BC，
∴∠ADG+∠GDB=90°．
∵四边形EFGD为正方形，
∴DE=DG，且∠GDE=90°，
∴∠ADG+∠ADE=90°，
∴∠BDG=∠ADE．
在△BDG和△ADE中，
$\left\{\begin{array}{l}{BD=AD}\\{∠BDG=∠ADE}\\{GD=ED}\end{array}\right.$，
∴△BDG≌△ADE（SAS），
∴BG=AE，
∠AED=∠BGD，
∴∠BGD+DMG=90°，∠DMG=∠EMN
∴∠EMN+∠AED=90°，
∴BG⊥AE．

点评 本题考查了旋转的性质的运用，等腰直角三角形的性质的运用，勾股定理的运用，全等三角形的判定及性质的运用，正方形的性质的运用，解答时证明三角形全等是关键．