题目内容
1.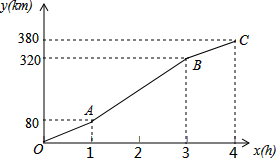 暑假期间,小刚一家乘车去离家380km的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.
暑假期间,小刚一家乘车去离家380km的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的函数图象如图所示.(1)分别求当x≤1、1<x≤3时,y关于x的函数表达式;
(2)小刚一家出发2.5h时离目的地多远?
分析 (1)当x≤1时,设y1=k1x,将A(1,80)代入,运用待定系数法求解;当1<x≤3时,设y2=k2x+b,将A、B两点的坐标代入,运用待定系数法即可求解;
(2)先将x=2.5代入AB段图象的函数表达式,求出对应的y值,进一步即可求解.
解答 解:(1)当x≤1时,设y1=k1x,
将A(1,80)代入,得k1=80,所以y1=80x;
当1<x≤3时,设y2=k2x+b,
∵A(1,80),B(3,320)在图象上,
∴$\left\{\begin{array}{l}{{k}_{2}+b=80}\\{3{k}_{2}+b=320}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{k}_{2}=120}\\{b=-40}\end{array}\right.$.
∴y2=120x-40(1<x≤3);
(2)当x=2.5时,y=120×2.5-40=260,
380-260=120(km).
故小刚一家出发2.5小时时离目的地120km远.
点评 本题考查了一次函数的应用及一次函数解析式的确定,解题的关键是通过仔细观察图象,从中整理出解题时所需的相关信息,本题较简单.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
9.已知函数y=$\sqrt{2x-4}$在实数范围内有意义,则自变量x的取值范围是( )
| A. | x≥2 | B. | x>2 | C. | x≤2 | D. | x<2 |
16.下列反比例函数中,图象经过点(1,-1)的是( )
| A. | y=$\frac{1}{x}$ | B. | y=$\frac{-1}{x}$ | C. | y=$\frac{2}{x}$ | D. | y=$\frac{-2}{x}$ |
 如图,AD与BE相交于F,∠A=∠C,∠1与∠2互补.
如图,AD与BE相交于F,∠A=∠C,∠1与∠2互补. 暑假就要来了,小明为自己制定了慢跑锻炼计划,某日小明从家出发沿解放路慢跑,已知他离家的距离s(千米)与时间t(分钟)之间的关系如图所示,请根据图象直接回答下列问题:
暑假就要来了,小明为自己制定了慢跑锻炼计划,某日小明从家出发沿解放路慢跑,已知他离家的距离s(千米)与时间t(分钟)之间的关系如图所示,请根据图象直接回答下列问题: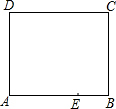 如图是一张长方形纸片ABCD,若AB=8,AD=6,E为AB上的一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是5或4$\sqrt{5}$或5$\sqrt{2}$.
如图是一张长方形纸片ABCD,若AB=8,AD=6,E为AB上的一点,AE=5,现要剪下一张等腰三角形纸片(△AEP),使点P落在长方形ABCD的某一条边上,则等腰三角形AEP的底边长是5或4$\sqrt{5}$或5$\sqrt{2}$.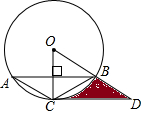 已知:如图,△ABC内接于⊙O,且半径OC⊥AB,点D在半径OB的延长线上,且∠A=∠BCD=30°,AC=2,则由$\widehat{BC}$,线段CD和线段BD所围成图形的阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.
已知:如图,△ABC内接于⊙O,且半径OC⊥AB,点D在半径OB的延长线上,且∠A=∠BCD=30°,AC=2,则由$\widehat{BC}$,线段CD和线段BD所围成图形的阴影部分的面积为2$\sqrt{3}$-$\frac{2}{3}$π.