题目内容
2．
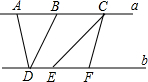如图，已知直线a∥b，点A、B、C在直线a上，点D、E、F在直线b上，AB=EF=2，若△CEF的面积为5，则△ABD的面积为（ ）| A． | 2 | B． | 4 | C． | 5 | D． | 10 |
分析 △CEF与△ABD是等底等高的两个三角形，它们的面积相等．
解答 解：∵直线a∥b，点A、B、C在直线a上，
∴点D到直线a的距离与点C到直线B的距离相等．
又∵AB=EF=2，
∴△CEF与△ABD是等底等高的两个三角形，
∴S△ABD=S△CEF=5，
故选：C．
点评 本题考查了平行线间的距离和三角形的面积．注意：平行线间的距离处处相等．
练习册系列答案
相关题目
13．一元二次方程x2+2x-5=0根的情况是（ ）
| A． | 无实数根 | B． | 有两个不相等的实数根 | ||
| C． | 只有一个实数根 | D． | 有两个相等的实数根 |
10．郑萌用已知线段a，b（a＞b，且$\sqrt{2}$b≠a），根据下列步骤作△ABC，则郑萌所作的三角形是（ ）
步骤：
①作线段AB=a；
②作线段AB的垂直平分线MN，交AB于点O；
③以点B为圆心，线段b的长为半径画弧，交⊙O于点C，连接BC，AC．
步骤：
①作线段AB=a；
②作线段AB的垂直平分线MN，交AB于点O；
③以点B为圆心，线段b的长为半径画弧，交⊙O于点C，连接BC，AC．
| A． | 等腰三角形 | B． | 等边三角形 | C． | 直角三角形 | D． | 钝角三角形 |
11．在方程组$\left\{\begin{array}{l}{x+2y=4k}\\{2x+y=2k+1}\end{array}\right.$中，若未知数x、y满足x-y＞0，则k的取值范围是（ ）
| A． | k$＞\frac{1}{2}$ | B． | k$＜\frac{1}{2}$ | C． | k$＞-\frac{1}{2}$ | D． | k$＜-\frac{1}{2}$ |