题目内容
11.在方程组$\left\{\begin{array}{l}{x+2y=4k}\\{2x+y=2k+1}\end{array}\right.$中,若未知数x、y满足x-y>0,则k的取值范围是( )| A. | k$>\frac{1}{2}$ | B. | k$<\frac{1}{2}$ | C. | k$>-\frac{1}{2}$ | D. | k$<-\frac{1}{2}$ |
分析 将方程组中两方程相减,便可得到关于x-y的方程,再根据x-y>0,即可求出k的取值范围.
解答 解:(2)-(1)得,(2x+y)-(x+2y)=2k+1-4k,
即x-y=1-2k,
∵x-y>0,即1-2k>0,故k<0.5,
故选B
点评 此题考查的是二元一次方程组和不等式的性质,要注意x-y>0,则解出x,y关于k的式子,最终求出k的取值范围.

练习册系列答案
 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
1.如果α是锐角,则下列成立的是( )
| A. | sinα+cosα=1 | B. | sinα+cosα>1 | C. | sinα+cosα<1 | D. | sinα+cosα≤1 |
 如图,在边长为1的小正方形网格中,△ABC的三个顶点都在格点上,将△ABC绕点B逆时针旋转90°得到△A′B′C′,则图中阴影部分图形的面积为$\frac{13}{4}π-3$.(结果保留π).
如图,在边长为1的小正方形网格中,△ABC的三个顶点都在格点上,将△ABC绕点B逆时针旋转90°得到△A′B′C′,则图中阴影部分图形的面积为$\frac{13}{4}π-3$.(结果保留π).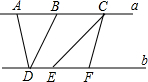 如图,已知直线a∥b,点A、B、C在直线a上,点D、E、F在直线b上,AB=EF=2,若△CEF的面积为5,则△ABD的面积为( )
如图,已知直线a∥b,点A、B、C在直线a上,点D、E、F在直线b上,AB=EF=2,若△CEF的面积为5,则△ABD的面积为( ) 在平面直角坐标系中,描出点A(0,2),B(-1,0),过点A作直线l1∥x轴,过点B作l2∥y轴,分析l1,l2上点的坐标特点.由此,你能总结出什么规律?
在平面直角坐标系中,描出点A(0,2),B(-1,0),过点A作直线l1∥x轴,过点B作l2∥y轴,分析l1,l2上点的坐标特点.由此,你能总结出什么规律?