题目内容
12.有一列数:a1,a2,a3,a4,…,若a1=1,$\frac{{a}_{2}}{{a}_{1}}$=$\frac{{a}_{3}}{{a}_{2}}$=$\frac{{a}_{4}}{{a}_{3}}$=…=2,则a2014=22013.分析 根据给定数列的特征可将a2014=$\frac{{a}_{2014}}{{a}_{2013}}$×$\frac{{a}_{2013}}{{a}_{2012}}$×…×$\frac{{a}_{3}}{{a}_{2}}$×$\frac{{a}_{2}}{{a}_{1}}$×a1,代入数据即可得出结论.
解答 解:a2014=$\frac{{a}_{2014}}{{a}_{2013}}$×$\frac{{a}_{2013}}{{a}_{2012}}$×…×$\frac{{a}_{3}}{{a}_{2}}$×$\frac{{a}_{2}}{{a}_{1}}$×a1=2×2×…×2×2×1=22014-1=22013.
故答案为:22013.
点评 本题考查了规律题型中的数字的变化,解题的关键是:根据数列的特征,将a2014转化为2014个代数式相乘的形式.本题难度不大,但不少同学会在计算过程中误以为a2014中有2014个2,从而得出错误的结论.这就要求同学们注意观察首位项的下标,断定有几个2.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
17.若二次函数y=x2+bx+5配方后为y=(x-2)2+k,则b、k的值分别为( )
| A. | 0 5 | B. | 0 1 | C. | -4 5 | D. | -4 1 |
1.如果α是锐角,则下列成立的是( )
| A. | sinα+cosα=1 | B. | sinα+cosα>1 | C. | sinα+cosα<1 | D. | sinα+cosα≤1 |
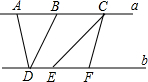 如图,已知直线a∥b,点A、B、C在直线a上,点D、E、F在直线b上,AB=EF=2,若△CEF的面积为5,则△ABD的面积为( )
如图,已知直线a∥b,点A、B、C在直线a上,点D、E、F在直线b上,AB=EF=2,若△CEF的面积为5,则△ABD的面积为( ) 在平面直角坐标系中,描出点A(0,2),B(-1,0),过点A作直线l1∥x轴,过点B作l2∥y轴,分析l1,l2上点的坐标特点.由此,你能总结出什么规律?
在平面直角坐标系中,描出点A(0,2),B(-1,0),过点A作直线l1∥x轴,过点B作l2∥y轴,分析l1,l2上点的坐标特点.由此,你能总结出什么规律? 如图,这是某邮递员投递区域街道图,现在,他要把一封电报从邮政局所在的O地尽快到A地,他所走的一条路线可用(0,0)→(0,3)→(4,3)→(4,8)→(7,8)表示,请你用这种形式出由O地到A地的其他几条路线.
如图,这是某邮递员投递区域街道图,现在,他要把一封电报从邮政局所在的O地尽快到A地,他所走的一条路线可用(0,0)→(0,3)→(4,3)→(4,8)→(7,8)表示,请你用这种形式出由O地到A地的其他几条路线.