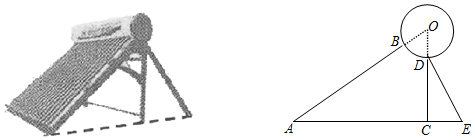题目内容
2.已知△ABC的外心为O,内心为I,∠BOC=120°,∠BIC=120°或150°.分析 用三角形外心的性质得出∠A的度数,再利用三角形内角和定理以及三角形内心的性质得出答案
解答 解:如图1,当△ABC是锐角三角形,
∵点O为△ABC的外心,∠BOC=120°,
∴∠A=60°,
∵点I为△ABC的内心,
∴∠ABC+∠ACB=120°,则∠IBC+∠ICB=60°,
∴∠BIC=120°.
如图2,当△ABC是钝角三角形,
∵∠BOC=120°,
∴∠A=120°,
∴∠IBC+∠ICB=30°,
∴∠BIC=150°.
故答案为:120°或150°.
点评 此题主要考查了三角形的内心与外心,解题的关键是正确画出图形,得出∠A的度数是解题关键,学会用分类讨论的思考问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 下列俯视图正确的是( )
下列俯视图正确的是( )
 下列俯视图正确的是( )
下列俯视图正确的是( )| A. |  | B. |  | C. |  | D. |  |
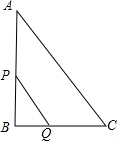 如图,在Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两点P,Q分别从点A和点C同时出发,沿边AB,CB向终点B移动.其中点P,Q的速度分别为2cm/s,1cm/s,且当其中一点到达终点时,另一点也随之停止移动.设P,Q两点移动时间为x s.
如图,在Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两点P,Q分别从点A和点C同时出发,沿边AB,CB向终点B移动.其中点P,Q的速度分别为2cm/s,1cm/s,且当其中一点到达终点时,另一点也随之停止移动.设P,Q两点移动时间为x s. 如图,已知一次函数y1=$\frac{4}{3}$x-4与反比例函数y2=$\frac{k}{x}$的图象在第一象限相交于点A(6,n),与x轴相交于点B.
如图,已知一次函数y1=$\frac{4}{3}$x-4与反比例函数y2=$\frac{k}{x}$的图象在第一象限相交于点A(6,n),与x轴相交于点B.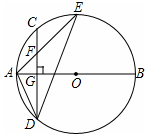 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{DF}=\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=3,AF=4.
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{DF}=\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=3,AF=4.