题目内容
3. 实数a、b、c在数轴上对应点的位置如图所示,则化简$\sqrt{(-a)^{2}}+\sqrt{(c-b)^{2}}-\sqrt{(a+c)^{2}}$的结果为( )
实数a、b、c在数轴上对应点的位置如图所示,则化简$\sqrt{(-a)^{2}}+\sqrt{(c-b)^{2}}-\sqrt{(a+c)^{2}}$的结果为( )| A. | -2a+b | B. | 2a-b+2c | C. | b | D. | -b |
分析 根据实数a、b、c在数轴上对应点的位置可得出c<a<0<b,进而求出-a>0,c-b<0,a+c<0,然后进行化简求解即可.
解答 解:$\sqrt{(-a)^{2}}+\sqrt{(c-b)^{2}}-\sqrt{(a+c)^{2}}$
=|-a|+|c-b|-|a+c|
=-a-(c-b)+(a+c)
=-a-c+b+a+c
=b.
故选C.
点评 本题考查了二次根式的性质与化简,解答本题的关键在于根据实数a、b、c在数轴上对应点的位置可得出c<a<0<b,进而求出-a>0,c-b<0,a+c<0.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目


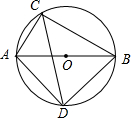 如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D.
如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D.