题目内容
13.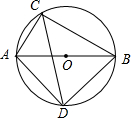 如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D.
如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D.(1)求弧BC的长;
(2)求弧BD的长.
分析 (1)首先根据AB是⊙O的直径,可得∠ACB=∠ADB=90°,然后在Rt△ABC中,求出∠BAC的度数,即可求出∠BOC的度数;最后根据弧长公式,求出$\widehat{BC}$的长即可.
(2)根据∠ACB的平分线交⊙O于点D确定AD=BD,从而求得∠BOD=∠AOD=90°,最后根据弧长公式,求出$\widehat{BD}$的长即可.
解答 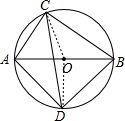 解:(1)如图,连接OC,OD,
解:(1)如图,连接OC,OD,
∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°,
在Rt△ABC中,
∵cos∠BAC=$\frac{AC}{AB}$=$\frac{5}{10}$=$\frac{1}{2}$,
∴∠BAC=60°,
∴∠BOC=2∠BAC=2×60°=120°,
∴$\widehat{BC}$的长=$\frac{120π×5}{180}$=$\frac{10}{3}$π.
(2)∵∠ACB的平分线交⊙O于点D,
∴∠DCA=∠BCD,
∴$\widehat{AD}$=$\widehat{BD}$,
∴AD=BD,
∴∠BOD=∠AOD=90°,
∴$\widehat{BD}$的长=$\frac{90π×5}{180}$=$\frac{5}{2}$π.
点评 此题主要考查了圆周角定理,含30度角的直角三角形,以及等腰直角三角形的性质和应用,还考查了弧长的求法,要熟练掌握,解答此题的关键是熟练掌握性质定理以及公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3. 实数a、b、c在数轴上对应点的位置如图所示,则化简$\sqrt{(-a)^{2}}+\sqrt{(c-b)^{2}}-\sqrt{(a+c)^{2}}$的结果为( )
实数a、b、c在数轴上对应点的位置如图所示,则化简$\sqrt{(-a)^{2}}+\sqrt{(c-b)^{2}}-\sqrt{(a+c)^{2}}$的结果为( )
 实数a、b、c在数轴上对应点的位置如图所示,则化简$\sqrt{(-a)^{2}}+\sqrt{(c-b)^{2}}-\sqrt{(a+c)^{2}}$的结果为( )
实数a、b、c在数轴上对应点的位置如图所示,则化简$\sqrt{(-a)^{2}}+\sqrt{(c-b)^{2}}-\sqrt{(a+c)^{2}}$的结果为( )| A. | -2a+b | B. | 2a-b+2c | C. | b | D. | -b |
5.下列各数中,负数是( )
| A. | (-5)2 | B. | -(-5) | C. | -|-5| | D. | -(-5)3 |
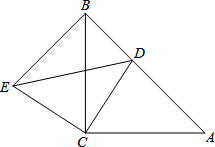 如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠ECD=90°,点D在AB上,连接BE.
如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠ECD=90°,点D在AB上,连接BE.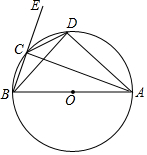 如图,已知AB是⊙O的直径,C、D均在⊙O上,点E在BC的延长线上,CD平分∠ACE
如图,已知AB是⊙O的直径,C、D均在⊙O上,点E在BC的延长线上,CD平分∠ACE 如图,在△ABC中,点D,E分别在边AB、AC上,DE∥BC.已知AE=6,$\frac{AD}{DB}$=$\frac{3}{4}$,则AC的长等于( )
如图,在△ABC中,点D,E分别在边AB、AC上,DE∥BC.已知AE=6,$\frac{AD}{DB}$=$\frac{3}{4}$,则AC的长等于( )
 一张直角三角形纸片ABC,∠C=90°,AB=24,tanB=$\frac{2}{3}$(如图),将它折叠使直角顶点C与斜边AB的中点重合,那么折痕的长为13.
一张直角三角形纸片ABC,∠C=90°,AB=24,tanB=$\frac{2}{3}$(如图),将它折叠使直角顶点C与斜边AB的中点重合,那么折痕的长为13.