题目内容
8.看图回答问题:
(1)内角和为2016°,佳佳为什么说不可能?
(2)音音求的是几边形的内角和?
分析 (1)根据n边形的内角和一定是180度的倍数,进行判断即可;
(2)设漏加的内角为x,得出方程(n-2)•180=2016+x,求得x=180n-2376,再根据90<x<180,得到90<180n-2376<180,最后求得n的范围即可.
解答 解:(1)∵n边形的内角和是(n-2)•180°,
∴内角和一定是180度的倍数,
∵2016÷180=11余36,
∴内角和为2016°不可能;
(2)设漏加的内角为x,依题意有
(n-2)•180=2016+x,
∴x=180n-2376,
∵90<x<180,
∴90<180n-2376<180,
解得13.7<n<14.2,
因而多边形的边数是14,
故音音求的是十四边形的内角和.
点评 本题主要考查了多边形的内角和与外角和,解决问题的关键是掌握多边形的内角和公式的运用,解题时注意:多边形的内角和是180°的整数倍.

练习册系列答案
相关题目
18. 如图,三角板的直角顶点在直线l上,若∠1=34°,则∠2的度数是( )
如图,三角板的直角顶点在直线l上,若∠1=34°,则∠2的度数是( )
 如图,三角板的直角顶点在直线l上,若∠1=34°,则∠2的度数是( )
如图,三角板的直角顶点在直线l上,若∠1=34°,则∠2的度数是( )| A. | 34° | B. | 68° | C. | 56° | D. | 146° |
19.比较下列数:1,-5,0,-1的大小,正确的是( )
| A. | -1<-5<0<1 | B. | -5<-1<0<1 | C. | 1<0<-1<-5 | D. | 0<-5<-1<1 |
16.在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍不一定能保证△ABC≌△A′B′C′( )
| A. | AB=B'C' | B. | ∠A=∠A′ | C. | AC=A′C′ | D. | ∠C=∠C′ |
3. 实数a、b、c在数轴上对应点的位置如图所示,则化简$\sqrt{(-a)^{2}}+\sqrt{(c-b)^{2}}-\sqrt{(a+c)^{2}}$的结果为( )
实数a、b、c在数轴上对应点的位置如图所示,则化简$\sqrt{(-a)^{2}}+\sqrt{(c-b)^{2}}-\sqrt{(a+c)^{2}}$的结果为( )
 实数a、b、c在数轴上对应点的位置如图所示,则化简$\sqrt{(-a)^{2}}+\sqrt{(c-b)^{2}}-\sqrt{(a+c)^{2}}$的结果为( )
实数a、b、c在数轴上对应点的位置如图所示,则化简$\sqrt{(-a)^{2}}+\sqrt{(c-b)^{2}}-\sqrt{(a+c)^{2}}$的结果为( )| A. | -2a+b | B. | 2a-b+2c | C. | b | D. | -b |
20. 如图,AB是⊙O的直径,∠ABC=30°,则∠BAC的度数是( )
如图,AB是⊙O的直径,∠ABC=30°,则∠BAC的度数是( )
 如图,AB是⊙O的直径,∠ABC=30°,则∠BAC的度数是( )
如图,AB是⊙O的直径,∠ABC=30°,则∠BAC的度数是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
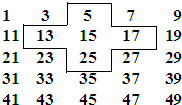 将连续的奇数1,3,5,7,9,…,排成如图所示的数阵.
将连续的奇数1,3,5,7,9,…,排成如图所示的数阵. 如图,在△ABC中,点D,E分别在边AB、AC上,DE∥BC.已知AE=6,$\frac{AD}{DB}$=$\frac{3}{4}$,则AC的长等于( )
如图,在△ABC中,点D,E分别在边AB、AC上,DE∥BC.已知AE=6,$\frac{AD}{DB}$=$\frac{3}{4}$,则AC的长等于( )