题目内容
15．观察下列算式：1×5+4=32，2×6+4=42，3×7+4=52，4×8+4=62，请你在观察规律之后，则这第n个式子是n（n+4）+4=（n+2）2．分析 观察一系列等式，归纳总结即可得到结果．
解答 解：∵1×5+4=32，2×6+4=42，3×7+4=52，4×8+4=62，
∴第n个算式为：n（n+4）+4=（n+2）2，
故答案为：n（n+4）+4=（n+2）2．
点评 本题主要考查了数字变化规律，根据数字变化得出数字规律是解题关键．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
3．
实数a、b、c在数轴上对应点的位置如图所示，则化简$\sqrt{（-a）^{2}}+\sqrt{（c-b）^{2}}-\sqrt{（a+c）^{2}}$的结果为（ ）
实数a、b、c在数轴上对应点的位置如图所示，则化简$\sqrt{（-a）^{2}}+\sqrt{（c-b）^{2}}-\sqrt{（a+c）^{2}}$的结果为（ ）| A． | -2a+b | B． | 2a-b+2c | C． | b | D． | -b |
10．下列各式中，与3-19+5的值相等的是（ ）
| A． | 3+（-19）-（-5） | B． | -3+（-19）+（-5） | C． | -3+（-19）+5 | D． | 3-（+19）-（+5） |
20．
如图，AB是⊙O的直径，∠ABC=30°，则∠BAC的度数是（ ）
如图，AB是⊙O的直径，∠ABC=30°，则∠BAC的度数是（ ）| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
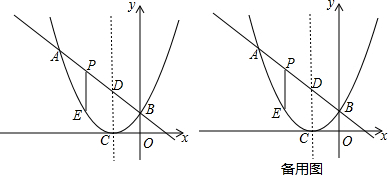
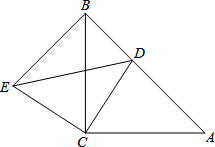如图，△ABC与△CDE均是等腰直角三角形，∠ACB=∠ECD=90°，点D在AB上，连接BE．
5．下列各数中，负数是（ ）
| A． | （-5）2 | B． | -（-5） | C． | -|-5| | D． | -（-5）3 |