题目内容
10.一次函数y=$\frac{4}{3}$x-b与y=$\frac{4}{3}$x-1的图象之间的距离等于3,则b的值为( )| A. | -2或4 | B. | 2或-4 | C. | 4或-6 | D. | -4或6 |
分析 设直线y=$\frac{4}{3}$x-1与x轴交点为C,与y轴交点为A,过点A作AD⊥直线y=$\frac{4}{3}$x-b于点D,根据直线的解析式找出点A、B、C的坐标,通过同角的余角相等可得出∠BAD=∠ACO,再利用∠ACO的余弦值即可求出直线AB的长度,从而得出关于b的含绝对值符号的方程,解方程即可得出结论.
解答 解:设直线y=$\frac{4}{3}$x-1与x轴交点为C,与y轴交点为A,过点A作AD⊥直线y=$\frac{4}{3}$x-b于点D,如图所示.
∵直线y=$\frac{4}{3}$x-1与x轴交点为C,与y轴交点为A,
∴点A(0,-1),点C($\frac{3}{4}$,0),
∴OA=1,OC=$\frac{3}{4}$,AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=$\frac{5}{4}$,
∴cos∠ACO=$\frac{OC}{AC}$=$\frac{3}{5}$.
∵∠BAD与∠CAO互余,∠ACO与∠CAO互余,
∴∠BAD=∠ACO.
∵AD=3,cos∠BAD=$\frac{AD}{AB}$=$\frac{3}{5}$,
∴AB=5.
∵直线y=$\frac{4}{3}$x-b与y轴的交点为B(0,-b),
∴AB=|-b-(-1)|=5,
解得:b=-4或b=6.
故选D.
点评 本题考查了一次函数的性质以及含绝对值符合的一元一次方程,解题的关键是找出线段AB=|-b-(-1)|=5.本题属于基础题,难度不大,解决该题型题目时,巧妙的借用角的余弦值求出线段AB的长度,再根据线段的长度得出关于b的含绝对值符号的方程是关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
1. 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
 如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )
如图,△ABC中,AD是中线,BC=8,∠B=∠DAC,则线段AC的长为( )| A. | 4 | B. | 4$\sqrt{2}$ | C. | 6 | D. | 4$\sqrt{3}$ |
 如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=$3\sqrt{2}$,CD=$2\sqrt{2}$,点P是四边形ABCD四条边上的一个动点,若P到BD的距离为$\frac{5}{2}$,则满足条件的点P有2个.
如图,四边形ABCD中,∠BAD=∠ADC=90°,AB=AD=$3\sqrt{2}$,CD=$2\sqrt{2}$,点P是四边形ABCD四条边上的一个动点,若P到BD的距离为$\frac{5}{2}$,则满足条件的点P有2个.
 如图,已知直线l1∥l2,将等边三角形如图放置,若∠α=40°,则∠β等于20°.
如图,已知直线l1∥l2,将等边三角形如图放置,若∠α=40°,则∠β等于20°. 如图,矩形纸片ABCD中,AB=4,BC=6.将该矩形纸片剪去3个等腰直角三角形,所有剪法中剩余部分面积的最小值是( )
如图,矩形纸片ABCD中,AB=4,BC=6.将该矩形纸片剪去3个等腰直角三角形,所有剪法中剩余部分面积的最小值是( )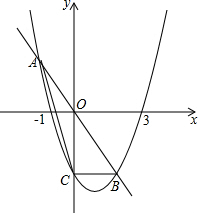 已知抛物线y=ax2+bx-3经过(-1,0),(3,0)两点,与y轴交于点C,直线y=kx与抛物线交于A,B两点.
已知抛物线y=ax2+bx-3经过(-1,0),(3,0)两点,与y轴交于点C,直线y=kx与抛物线交于A,B两点.