题目内容
14．
如图，在△ABC中，AB=AC，AD⊥BC，垂足为D，且BC=6cm，则BD=（ ）| A． | 1cm | B． | 2cm | C． | 3cm | D． | 4cm |
分析 由在△ABC中，AB=AC，AD⊥BC，根据三线合一的性质求解即可求得BD的长．
解答 解：∵AB=AC，AD⊥BC，
∴BD=$\frac{1}{2}$BC=$\frac{1}{2}$×6=3（cm）．
故选C．
点评 此题考查了等腰三角形的性质．注意等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
4．下列各数中，互为相反数的是（ ）
| A． | -32与23 | B． | 32与（-2）3 | C． | （-3）2与-32 | D． | -32与-（-3）2 |
5．设A=3x2-x+1，B=2x2-x-1，若x取任意实数，则A与B的大小关系为（ ）
| A． | A＞B | B． | A=B | C． | A＜B | D． | 无法比较 |
如图，在平行四边形ABCD中，AB=4cm，AD=7cm，∠ABC的角平分线交AD于点E，交CD的延长线于点F，则DE=3cm．
如图所示，已知AB=AC，在△ABD与△ACD中，要使△ABD≌△ACD，还需要再添加一个条件是AD平分∠BAC．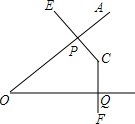
如图，已知∠AOB，其中CE⊥OA于点P，CF⊥OB于点Q．