Question

4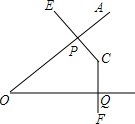．如图，已知∠AOB，其中CE⊥OA于点P，CF⊥OB于点Q．
（1）求证：∠AOB与∠ECF互补．
（2）由（1）小莹得出结论：如果一个角的两边与另一个角的两边互相垂直，那么这两个角互补，你认为她的想法正确吗？为什么？

Answer 1

分析 （1）利用四边形内角和定理结合垂线的定义得出：∠AOB与∠ECF互补；
（2）可以通过两个图形得出这两个角的关系相等或互补．

解答 （1）证明：如图1，∵CE⊥OA于点P，CF⊥OB于点Q，
∴∠OPC=∠OQC=90°，
∴∠AOB+∠ECF=360°-90°-90°=180°，
即∠AOB与∠ECF互补；

（2）解：她的想法不正确，
理由：如图2：根据垂直的量相等的角都等于90°，对顶角相等，所以∠1=∠2，
再由（1）得：如果一个角的两边与另一个角的两边互相垂直，那么这两个角互补或相等．

点评 此题考查了垂线以及补角的定义，关键明确四边形的内角和等于360°，三角形的内角和等于180°，对顶角相等的性质，对图形准确分析利用是解题的关键．