题目内容
12. 如图,在△ABC中,∠B=∠C,点D、E、F分别在AB、BC、AC上,且BD=CE,∠DEF=∠B,求证:△BDE≌△CEF.
如图,在△ABC中,∠B=∠C,点D、E、F分别在AB、BC、AC上,且BD=CE,∠DEF=∠B,求证:△BDE≌△CEF.
分析 首先证明∠BDE=∠FEC,然后再利用ASA定理判定△BDE≌△CEF即可.
解答 证明:∵∠DEF=∠B,∠B=∠C,∠B+∠BDE+∠DEB=180°,∠DEB+∠DEF+∠FEC=180°,
∴∠BDE=∠FEC,
在△BDE和△CEF中$\left\{\begin{array}{l}{∠B=∠C}\\{BD=CE}\\{∠BDE=∠FEC}\end{array}\right.$,
∴△BDE≌△CEF(ASA).
点评 此题主要考查了三角形全等的判定,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.2010年3月份,某市市区一周空气质量报告中某项污染指数的数据是:31,35,31,34,30,32,31,这组数据的中位数、众数分别是( )
| A. | 32,31 | B. | 31,32 | C. | 31,31 | D. | 32,35 |
4.与方程组$\left\{\begin{array}{l}{x+3y=-3}\\{x+y=-2}\end{array}\right.$有相同解的方程组是( )
| A. | $\left\{\begin{array}{l}{x-y=1}\\{3x=5-y}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=y-1}\\{3x=5-y}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=y-1}\\{3x+5+y=0}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=y-1}\\{3x+5-y=0}\end{array}\right.$ |




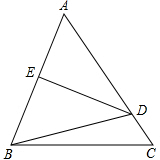 如图所示,△ABC为等腰三角形,AB=AC,AE=BE,AD=BD,∠DBC=15°,求∠ADE的度数.
如图所示,△ABC为等腰三角形,AB=AC,AE=BE,AD=BD,∠DBC=15°,求∠ADE的度数.