题目内容
1.解方程组:$\frac{3x+2y}{4}$=$\frac{x+5y}{-3}$=$\frac{2x+y+2}{5}$.分析 方程组整理后,利用加减消元法求出解即可.
解答 解:方程组整理得:$\left\{\begin{array}{l}{x+2y=0①}\\{11x+28y=-6②}\end{array}\right.$,
①×28-②得:17x=6,即x=$\frac{6}{17}$,
把x=$\frac{6}{17}$代入①得:y=-$\frac{3}{17}$,
则方程组的解为$\left\{\begin{array}{l}{x=\frac{6}{17}}\\{y=-\frac{3}{17}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
9.已知关于x的方程$\frac{x+a}{x+2}$=-1的根是负数,则a的取值范围是( )
| A. | a<0且a≠-2 | B. | a>0且a≠2 | C. | a>-2且a≠2 | D. | a<2且a≠-2 |
10.一只不透明的袋子中装有1个白球,2个黄球和3个红球,每个球除颜色外都相同,将球搅匀,从中任意摸出一个球.如果想使摸到这三种颜色的球的概率相等,下列做法正确的是( )
| A. | 向袋子里分别投放1个白球,1个黄球,1个红球 | |
| B. | 向袋子里分别投放3个白球,2个黄球,1个红球 | |
| C. | 向袋子里分别投放2个白球,1个红球 | |
| D. | 向袋子里投放2个白球 |
11. 如图是函数y=$\frac{a}{x}$-1的图象,则关于x的分式方程$\frac{a}{x}$=3的解是( )
如图是函数y=$\frac{a}{x}$-1的图象,则关于x的分式方程$\frac{a}{x}$=3的解是( )
 如图是函数y=$\frac{a}{x}$-1的图象,则关于x的分式方程$\frac{a}{x}$=3的解是( )
如图是函数y=$\frac{a}{x}$-1的图象,则关于x的分式方程$\frac{a}{x}$=3的解是( )| A. | x=6 | B. | x=0.5 | C. | x=2 | D. | x=1 |
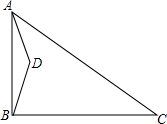 在△ABC中,∠ABC=90°,D为平面内一动点,AD=a,AC=b,其中a,b为常数,且a<b.将△ABD沿射线BC方向平移,得到△FCE,点A、B、D的对应点分别为点F、C、E.连接BE.
在△ABC中,∠ABC=90°,D为平面内一动点,AD=a,AC=b,其中a,b为常数,且a<b.将△ABD沿射线BC方向平移,得到△FCE,点A、B、D的对应点分别为点F、C、E.连接BE. 如图,在△ABC中,∠B=∠C,点D、E、F分别在AB、BC、AC上,且BD=CE,∠DEF=∠B,求证:△BDE≌△CEF.
如图,在△ABC中,∠B=∠C,点D、E、F分别在AB、BC、AC上,且BD=CE,∠DEF=∠B,求证:△BDE≌△CEF.