题目内容
4.若a,b都是有理数,且a2-2ab+2b2+4b+4=0,则$\sqrt{ab}$=2.分析 先利用配方法得到(a-b)2+(b+2)2=0,再利用非负数的性质得a-b=0,b+2=0,易得a=b=-2,然后根据算术平方根的定义求解.
解答 解:∵a2-2ab+2b2+4b+4=0,
∴a2-2ab+b2+b2+4b+4=0,
∴(a-b)2+(b+2)2=0,
∴a-b=0,b+2=0,
∴a=b=-2,
∴$\sqrt{ab}$=$\sqrt{(-2)×(-2)}$=2.
故答案为2.
点评 本题考查了配方法的应用:用配方法解一元二次方程;利用配方法求二次三项式是一个完全平方式时所含字母系数的值.也考查了非负数的性质.

练习册系列答案
相关题目
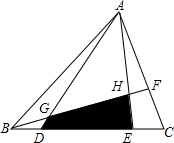 如图,在△ABC中,点D、E在BC上,且BD=EC=$\frac{1}{5}$BC,F在AC上,且AF=$\frac{2}{3}$AC,BF与AD、AE分别交于点G、H,若△ABC的面积为1155,求:
如图,在△ABC中,点D、E在BC上,且BD=EC=$\frac{1}{5}$BC,F在AC上,且AF=$\frac{2}{3}$AC,BF与AD、AE分别交于点G、H,若△ABC的面积为1155,求: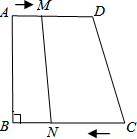 如图,梯形ABCD中,AD∥CB,∠B=90°,AD=18cm,BC=21cm,点M从点A开始沿AD向D点以1cm/s的速度移动,点N从点C开始沿CB边向点B以2cm/s的速度移动,则:
如图,梯形ABCD中,AD∥CB,∠B=90°,AD=18cm,BC=21cm,点M从点A开始沿AD向D点以1cm/s的速度移动,点N从点C开始沿CB边向点B以2cm/s的速度移动,则: