题目内容
9.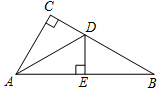 如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,DE⊥AB于点E.
如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,DE⊥AB于点E.(1)求证:△ACD≌△AED
(2)若AC=5,△DEB的周长为8,求△ABC的周长.
分析 (1)根据HL证明△ACD≌△AED即可;
(2)根据C△ABC=AC+AB+BC=AC+(AE+EB)+(BD+DC)=AC+AC+(EB+BD+DE)=AC+AC+C△DEB计算即可;
解答 解:(1)证明:因为AD平分∠CAB,∠C=90°,DE⊥AB
所以DC=DE
在△ACD和△AED中,
$\left\{\begin{array}{l}{DC=DE}\\{AD=AD}\end{array}\right.$,
∴△ACD≌△AED(HL).
(2)由(1)得△ACD≌△AED
所以AE=AC=5,CD=ED,
C△ABC=AC+AB+BC
=AC+(AE+EB)+(BD+DC)
=AC+AC+(EB+BD+DE)
=AC+AC+C△DEB
=5+5+8
=18.
点评 本题考查全等三角形的判定和性质、角平分线的性质定理等知识,解题的关键是掌握角平分线的性质定理,属于中考常考题型.

练习册系列答案
 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
14.四个内角都相等的四边形是( )
| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 正方形 |
1.已知点A(4,y1),B($\sqrt{2}$,y2),C(-2,y3)都在y=$\frac{9}{x}$上,试判断y1,y2,y3的大小关系( )
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y1<y3<y2 |
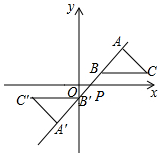 如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交x轴于点P.若△ABC与△A'B'C'关于点P成中心对称,则点A'的坐标为(-2,-3).
如图,在平面直角坐标系中,△ABC的顶点A在第一象限,点B,C的坐标为(2,1),(6,1),∠BAC=90°,AB=AC,直线AB交x轴于点P.若△ABC与△A'B'C'关于点P成中心对称,则点A'的坐标为(-2,-3). 如图,在?ABCD中,点E在DA的延长线上,点F在BC的延长线上,且BE∥FD.求证:∠ABE=∠CDF.
如图,在?ABCD中,点E在DA的延长线上,点F在BC的延长线上,且BE∥FD.求证:∠ABE=∠CDF.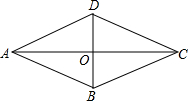 已知:如图,在四边形ABCD中,对角线AC、BD交于点O,线段BD垂直平分AC,DC∥AB.
已知:如图,在四边形ABCD中,对角线AC、BD交于点O,线段BD垂直平分AC,DC∥AB.