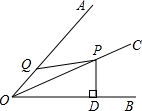
题目内容
10. 如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )| A. | PA=PB | B. | PO平分∠APB | C. | AB垂直平分OP | D. | ∠OBA=∠OAB |
分析 根据角平分线上的点到角的两边距离相等可得PA=PB,再利用“HL”证明△AOP和△BOP全等,根据全等三角形对应角相等可得∠AOP=∠BOP,全等三角形对应边相等可得OA=OB.
解答 解:∵OP平分∠AOB,PA⊥OA,PB⊥OB,
∴PA=PB,故A选项正确;
在△AOP和△BOP中,
$\left\{\begin{array}{l}{PO=PO}\\{PA=PB}\end{array}\right.$,
∴△AOP≌△BOP(HL),
∴∠AOP=∠BOP,OA=OB,故B选项正确;
由等腰三角形三线合一的性质,OP垂直平分AB,AB不一定垂直平分OP,
即不一定成立的是选项C;
∵OA=OB,
∴∠OBA=∠OAB,故选项D正确;
故选C.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,熟记性质并求出两三角形全等是解题的关键.

练习册系列答案
相关题目
8.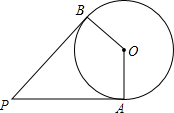 如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则$\widehat{AB}$的长为( )
如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则$\widehat{AB}$的长为( )
 如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则$\widehat{AB}$的长为( )
如图,PA、PB是⊙O的切线,切点分别为A、B,若OA=2,∠P=60°,则$\widehat{AB}$的长为( )| A. | $\frac{2}{3}$π | B. | π | C. | $\frac{4}{3}π$ | D. | $\frac{5}{3}π$ |
18.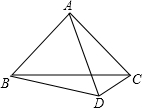 如图,△ABC是等腰直角三角形,∠BAD=60°,且AD=AB,则∠BCD=( )
如图,△ABC是等腰直角三角形,∠BAD=60°,且AD=AB,则∠BCD=( )
 如图,△ABC是等腰直角三角形,∠BAD=60°,且AD=AB,则∠BCD=( )
如图,△ABC是等腰直角三角形,∠BAD=60°,且AD=AB,则∠BCD=( )| A. | 30° | B. | 15° | C. | 45° | D. | 35° |
15.不等式$\left\{\begin{array}{l}{-x<3}\\{4x-8≤12}\end{array}\right.$的解集是( )
| A. | -3<x≤5 | B. | 3<x≤5 | C. | 3<x≤-5 | D. | -3<x<5 |
2.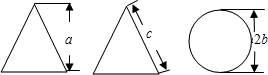 如图,是某几何体的三视图及相关数据,则下面判断正确的是( )
如图,是某几何体的三视图及相关数据,则下面判断正确的是( )
 如图,是某几何体的三视图及相关数据,则下面判断正确的是( )
如图,是某几何体的三视图及相关数据,则下面判断正确的是( )| A. | a>c | B. | b>c | C. | a2+4b2=c2 | D. | a2+b2=c2 |
20.下列关于“-1”的说法中,错误的是( )
| A. | -1的相反数是1 | B. | -1是最小的负整数 | ||
| C. | -1的绝对值是1 | D. | -1是最大的负整数 |