题目内容
1.某校校长寒假将带领该校市级三好学生去北京旅游,甲旅行社说:”如果校长买全票一张,则其余学生可享受半价优惠”.”乙旅行社说:”包括校长在内全部按全票价的6折优惠(即按全票价的60%收费)”,甲、乙旅行社的全票价都为240元,(1)设学生数为x,甲旅行社收费记为y,乙旅行社收费记为z,分别写出两家旅行社的收费y与x的函数关系式;
(2)当学生人数是多少时选择甲旅行社和选择乙旅行社所需费用一样多?
(3)若学生有6人,选择哪家旅行社更合算?
分析 (1)首先根据题意分别求得y、z与x的函数关系式,再进行整理化简;
(2)根据两家旅行社收费一样,列出方程进行求解;
(3)根据自变量x的取值为6,分别求得两个函数值,并进行比较.
解答 解:(1)根据题意,得
y=240+50%×240x=120x+240,
z=240×60%(x+1)=144x+144;
(2)当选择甲旅行社和选择乙旅行社所需费用一样多时,y=z,
即120x+240=144x+144
解得x=4.
∴当学生人数为4时,两家旅行社收费一样;
(3)甲旅行社共需要:240+120×6=240+720=960(元);
乙旅行社共需要:144×6+144=864+144=1008(元);
∴选择甲旅行社更合算.
点评 本题主要考查了一次函数的实际应用问题.此题难度适中,解题的关键是理解题意,根据等量关系求得一次函数,然后根据一次函数的表达式进行计算求解.

练习册系列答案
相关题目
9.在有理数-3,-1$\frac{1}{2}$,0.3,-1,-96,5.9中,整数有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
16.若一次函数y=kx-b的图象经过第二、三、四象限,则k,b的取值范围是( )
| A. | k>0,b>0 | B. | k<0,b>0 | C. | k<0,b<0 | D. | k<0,b>0 |
6.我们知道:31=3,32=9,33=27,34=81,35=243…;81=8,82=64,83=512,84=4096,85=32768…,那么1282015+632016结果的个位数字是( )
| A. | 1 | B. | 3 | C. | 5 | D. | 7 |
13.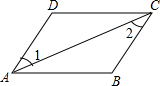 如图,在四边形ABCD中,若∠1=∠2,则AD∥BC,理由是( )
如图,在四边形ABCD中,若∠1=∠2,则AD∥BC,理由是( )
 如图,在四边形ABCD中,若∠1=∠2,则AD∥BC,理由是( )
如图,在四边形ABCD中,若∠1=∠2,则AD∥BC,理由是( )| A. | 两直线平行,内错角相等 | B. | 两直线平行,同位角相等 | ||
| C. | 内错角相等,两直线平行 | D. | 同位角相等,两直线平行 |
10. 如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
 如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )
如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中不一定成立的是( )| A. | PA=PB | B. | PO平分∠APB | C. | AB垂直平分OP | D. | ∠OBA=∠OAB |
11.关于x的一元二次方程x2-4sinα•x+2=0有两个等根,则锐角α的度数是( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
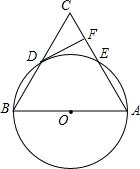 如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.
如图,在△ABC中,以AB为直径的⊙O分别与BC,AC相交于点D,E,BD=CD,过点D作⊙O的切线交边AC于点F.