题目内容
8.已知x=$\sqrt{c}$-$\sqrt{c-1}$,y=$\sqrt{c+1}$-$\sqrt{c}$,z=$\sqrt{c+2}$-$\sqrt{c+1}$,试比较x,y,z的大小.分析 作差得到x-y=(2$\sqrt{c}$)-($\sqrt{c-1}$+$\sqrt{c+1}$),被减数和减数平方,比较它们平方的大小;作差得到y-z=(2$\sqrt{c+1}$)-($\sqrt{c}$+$\sqrt{c+2}$),被减数和减数平方,比较它们平方的大小;进一步即可求解.
解答 解:∵x=$\sqrt{c}$-$\sqrt{c-1}$,y=$\sqrt{c+1}$-$\sqrt{c}$,z=$\sqrt{c+2}$-$\sqrt{c+1}$,
∴x-y=(2$\sqrt{c}$)-($\sqrt{c-1}$+$\sqrt{c+1}$),
(2$\sqrt{c}$)2=4c,
($\sqrt{c-1}$+$\sqrt{c+1}$)2=2c+2$\sqrt{{c}^{2}-1}$,
4c>2c+2$\sqrt{{c}^{2}-1}$,
∴x-y>0,
∴x>y;
y-z=(2$\sqrt{c+1}$)-($\sqrt{c}$+$\sqrt{c+2}$),
(2$\sqrt{c+1}$)2=4(c+1),
($\sqrt{c}$+$\sqrt{c+2}$)2=2(c+1)+2$\sqrt{c(c+2)}$,
4(c+1)>2(c+1)+2$\sqrt{c(c+2)}$,
∴y-z>0,
∴y>z,
∴x>y>z.
点评 此题考查了实数大小比较,任意两个实数都可以比较大小.正实数都大于0,负实数都小于0,正实数大于一切负实数,两个负实数绝对值大的反而小.关键是熟悉作差法比较大小的方法.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
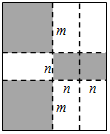 如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为m厘米的大正方形,两块是边长都为n厘米的小正方形,五块是长宽分别是m厘米、n厘米的全等小矩形,且m>n.
如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为m厘米的大正方形,两块是边长都为n厘米的小正方形,五块是长宽分别是m厘米、n厘米的全等小矩形,且m>n.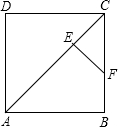 已知:如图,E是正方形ABCD对角线AC上一点,且AE=AB,EF⊥AC,交BC于F.求证:BF=EC.
已知:如图,E是正方形ABCD对角线AC上一点,且AE=AB,EF⊥AC,交BC于F.求证:BF=EC.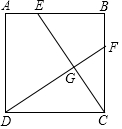 如图,正方形ABCD中,AE=BF.
如图,正方形ABCD中,AE=BF.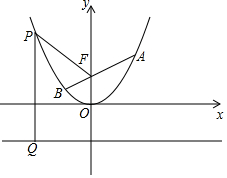 已知抛物线C:y=$\frac{1}{4}$x2+bx+c在x=1和x=-1时的函数值相等,且x=2时y=1,P(x,y)为抛物线C上任一点,F(0,1)为y轴上一点,PQ与直线y=-1垂直交于点Q
已知抛物线C:y=$\frac{1}{4}$x2+bx+c在x=1和x=-1时的函数值相等,且x=2时y=1,P(x,y)为抛物线C上任一点,F(0,1)为y轴上一点,PQ与直线y=-1垂直交于点Q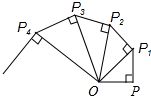 如图,OP=1,过P作PP1⊥OP,且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1,且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2,且P2P3=1,得OP3=2;…依此法继续作下去,得OP2016=$\sqrt{2017}$.
如图,OP=1,过P作PP1⊥OP,且PP1=1,得OP1=$\sqrt{2}$;再过P1作P1P2⊥OP1,且P1P2=1,得OP2=$\sqrt{3}$;又过P2作P2P3⊥OP2,且P2P3=1,得OP3=2;…依此法继续作下去,得OP2016=$\sqrt{2017}$.