题目内容
19.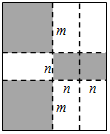 如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为m厘米的大正方形,两块是边长都为n厘米的小正方形,五块是长宽分别是m厘米、n厘米的全等小矩形,且m>n.
如图,将一张矩形大铁皮切割成九块,切痕如下图虚线所示,其中有两块是边长都为m厘米的大正方形,两块是边长都为n厘米的小正方形,五块是长宽分别是m厘米、n厘米的全等小矩形,且m>n.(1)用含m、n的代数式表示切痕的总长为6m+6n厘米;
(2)若每块小矩形的面积为48厘米2,四个正方形的面积和为200厘米2,试求(m+n)2的值.
分析 (1)根据切痕长有两横两纵列出算式,再根据合并同类项法则整理即可;
(2)根据小矩形的面积和正方形的面积列出算式,再利用完全平方公式整理求出m+n的值,即可得到结论.
解答 解:(1)切痕总长=2[(m+2n)+(2m+n)],
=6m+6n;
故答案为:6m+6n;
(2)由题意得:mn=48,m2+n2=100,
∴(m+n)2=m2+n2+2mn=196.
点评 本题考查对完全平方公式几何意义的理解,应从整体和部分两方面来理解完全平方公式的几何意义;主要围绕图形周长和面积展开分析.

练习册系列答案
相关题目

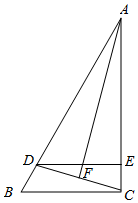 如图,在△ABC中,∠ACB=90°.D为AB上一点,且AC=AD.连接CD,过点D作DE∥BC.DE与AC相交于E.F为CD的中点,连接AF,EF.
如图,在△ABC中,∠ACB=90°.D为AB上一点,且AC=AD.连接CD,过点D作DE∥BC.DE与AC相交于E.F为CD的中点,连接AF,EF. 正方形ABCD中,点P为边AD上的一点,DE⊥CP于E,延长CP到F,使得CE=EF,连接DF、AF,过点D作∠ADF的角平分线,交CF于H,连结BH.
正方形ABCD中,点P为边AD上的一点,DE⊥CP于E,延长CP到F,使得CE=EF,连接DF、AF,过点D作∠ADF的角平分线,交CF于H,连结BH.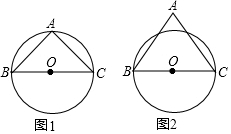 已知BC是⊙O的直径,△ABC为等腰三角形,请仅用无刻度的直尺完成下列作图.
已知BC是⊙O的直径,△ABC为等腰三角形,请仅用无刻度的直尺完成下列作图.