题目内容
3．
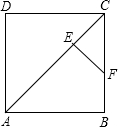已知：如图，E是正方形ABCD对角线AC上一点，且AE=AB，EF⊥AC，交BC于F．求证：BF=EC．
分析 如图连接AF．只要证明△ECF是等腰直角三角形，△AFE≌△AFB即可解决问题．
解答 解：如图连接AF．
∵四边形ABCD是正方形，
∴∠ACB=45°，
∵FE⊥AC，
∴∠AEF=∠CEF=∠B=90°，
∴∠ECF=∠EFC=45°，
∴EF=CE，
在Rt△AFE和Rt△AFB中，
$\left\{\begin{array}{l}{AF=AF}\\{AE=AB}\end{array}\right.$，
∴Rt△AFE≌Rt△AFB，
∴BF=EF=CE，
∴BF=EC．
点评 本题考查正方形的性质、全等三角形的判定和性质、等腰直角三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型．
练习册系列答案
相关题目
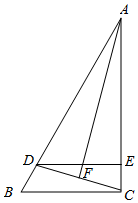如图，在△ABC中，∠ACB=90°．D为AB上一点，且AC=AD．连接CD，过点D作DE∥BC．DE与AC相交于E．F为CD的中点，连接AF，EF．
正方形ABCD中，点P为边AD上的一点，DE⊥CP于E，延长CP到F，使得CE=EF，连接DF、AF，过点D作∠ADF的角平分线，交CF于H，连结BH．
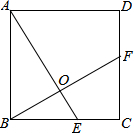如图，正方形ABCD中，E、F分别是AB、BC边上的点，且AE=BF．
如图，在平面直角坐标系中，二次函数y=ax2+bx+c的图象经过点A（-2，0），B（0，-2$\sqrt{3}$），C（4，0），其中对称轴与x轴交于点D．