题目内容
18．解方程：（1）$\left\{\begin{array}{l}{2x+3y=12①}\\{x-2y=-1②}\end{array}\right.$
（2）$\left\{\begin{array}{l}{6x-5y=4①}\\{2x-3y=4②}\end{array}\right.$．
分析 （1）根据加减消元法，由①-②×2消去x，求出y，再把y代入②求出x即可；
（2）根据加减消元法，由①-②×3消去x，求出y，再把y代入②求出x即可．
解答 解：（1）$\left\{\begin{array}{l}{2x+3y=12①}\\{x-2y=-1②}\end{array}\right.$，
①-②×2得7y=14，解得y=2，
把y=2代入②得x-4=-1，解得x=3．
故原方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$．
（2）$\left\{\begin{array}{l}{6x-5y=4①}\\{2x-3y=4②}\end{array}\right.$，
①-②×2得4y=8，解得y=-2，
把y=-2代入②得2x+6=4，解得x=-1．
故原方程组的解为$\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$．
点评 考查了解二元一次方程组，用加减法解二元一次方程组的一般步骤：①方程组的两个方程中，如果同一个未知数的系数既不相等又不互为相反数，就用适当的数去乘方程的两边，使某一个未知数的系数相等或互为相反数．②把两个方程的两边分别相减或相加，消去一个未知数，得到一个一元一次方程．③解这个一元一次方程，求得未知数的值．④将求出的未知数的值代入原方程组的任意一个方程中，求出另一个未知数的值．⑤把所求得的两个未知数的值写在一起，就得到原方程组的解，用$\left\{\begin{array}{l}{x=a}\\{y=b}\end{array}\right.$的形式表示．
练习册系列答案
相关题目
6．如图，它们是按一定规律排列的，依照此规律，第20个图形共有★的数量为（ ）
| A． | 63 | B． | 57 | C． | 68 | D． | 60 |
3．
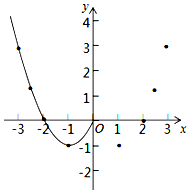某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究，探究过程如下．
（1）自变量x的取值范围是全体实数，x与y的几组对应值如下：
其中，m=0．
（2）根据表中数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请你画出该函数图象的另一部分．
（3）观察函数图象，写出一条性质．函数y=x2-2|x|的图象关于y轴对称
（4）进一步探究函数图象发现：
①方程x2-2|x|=0有3个实数根；
②关于x的方程x2-2|x|=a有4个实数根时，a的取值范围是-1＜a＜0．
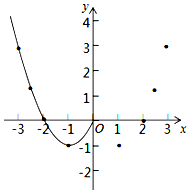某班“数学兴趣小组”对函数y=x2-2|x|的图象和性质进行了探究，探究过程如下．（1）自变量x的取值范围是全体实数，x与y的几组对应值如下：
| x | … | -3 | -$\frac{5}{2}$ | -2 | -1 | 0 | 1 | 2 | $\frac{5}{2}$ | 3 | … |
| y | … | 3 | $\frac{5}{4}$ | m | -1 | 0 | -1 | 0 | $\frac{5}{4}$ | 3 | … |
（2）根据表中数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请你画出该函数图象的另一部分．
（3）观察函数图象，写出一条性质．函数y=x2-2|x|的图象关于y轴对称
（4）进一步探究函数图象发现：
①方程x2-2|x|=0有3个实数根；
②关于x的方程x2-2|x|=a有4个实数根时，a的取值范围是-1＜a＜0．
