��Ŀ����
18��ij�̵�ͨ�����ͼ۸�ķ�ʽ����n����ͬ����ߣ�������ĵ���y��Ԫ�������ǰ�ĵ���x��Ԫ������һ�κ�����ϵ�������| ��1�� | ��2�� | ��3�� | ��4�� | �� | ��n�� | |
| ����ǰ�ĵ���x��Ԫ�� | x1 | x2=6 | x3=72 | x4 | �� | xn |
| ������ĵ���y��Ԫ�� | y1 | y2=4 | y3=59 | y4 | �� | yn |
��1����y��x�ĺ�����ϵʽ����ȷ��x��ȡֵ��Χ��
��2��ij����ߵ���ǰ������108Ԫ���˿���������ʡ�˶���Ǯ��
��3����n����ߵ���ǰ�����ƽ�����۷ֱ�Ϊ$\overline{x}$��$\overline{y}$������$\overline{y}$��$\overline{x}$�Ĺ�ϵʽ����д���Ƶ����̣�
���� ��1����y=kx+b�����������з����鼴�ɵõ����ۣ��ٸ�����֪�����õ�����ʽ���ǵõ�x��ȡֵ��Χ��x��$\frac{18}{5}$��
��2����x=108����y=$\frac{5}{6}$x-1���ɵõ����ۣ�
��3���ɣ�1����y1=$\frac{5}{6}$x1-1��y2=$\frac{5}{6}$x2-2����yn=$\frac{5}{6}$xn-1��������ƽ�����Ĺ�ʽ���ɵõ����ۣ�
��� �⣺��1����y=kx+b���������x=6��y=4��x=72��y=59��
��$\left\{\begin{array}{l}{4=6k+b}\\{59=72k+b}\end{array}\right.$
�����$\left\{\begin{array}{l}{k=\frac{5}{6}}\\{b=-1}\end{array}\right.$��
��y��x�ĺ�����ϵʽΪy=$\frac{5}{6}$x-1��
����n����ߵ�����ĵ��۶�����2Ԫ��
��$\frac{5}{6}$x-1��2�����x��$\frac{18}{5}$��
��x��ȡֵ��Χ��x��$\frac{18}{5}$��
��2����x=108����y=$\frac{5}{6}$x-1��y=$\frac{5}{6}$��108-1=89��
108-89=19��
�𣺹˿���������ʡ��19Ԫ��
��3��$\overline{y}$=$\frac{5}{6}$$\overline{x}$-1��
�Ƶ����̣��ɣ�1����y1=$\frac{5}{6}$x1-1��y2=$\frac{5}{6}$x2-1����yn=$\frac{5}{6}$xn-1��
��$\overline{y}$=$\frac{1}{n}$��y1+y2+��+yn��=$\frac{1}{n}$[��$\frac{5}{6}$x1-1��+��$\frac{5}{6}$x2-1��+��+��$\frac{5}{6}$xn-1��]=$\frac{1}{n}$[$\frac{5}{6}$��x1+x2+��+xn��-n]=$\frac{5}{6}$��$\frac{{x}_{1}+{x}_{2}+��+{x}_{n}}{n}$-1=$\frac{5}{6}$$\overline{x}$-1��
���� ���⿼����һ�κ�����Ӧ�ã������Ľ���ʽ�����һ�κ����������ǽ���Ĺؼ���

 ��ͼ����ABC�DZ߳�Ϊ1���������Σ���AB�ͻ�AC���Ե�Բ�ĽǾ�Ϊ120�㣬��ͼ����Ӱ���ֵ����Ϊ$\frac{\sqrt{3}}{12}$��
��ͼ����ABC�DZ߳�Ϊ1���������Σ���AB�ͻ�AC���Ե�Բ�ĽǾ�Ϊ120�㣬��ͼ����Ӱ���ֵ����Ϊ$\frac{\sqrt{3}}{12}$��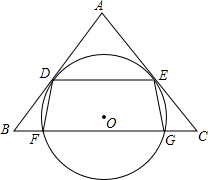 ��ͼ��O�ǡ�ABC��һ�㣬��O��BC�ཻ��F��G���㣬����AB��AC�ֱ������ڵ�D��E��DE��BC������DF��EG��
��ͼ��O�ǡ�ABC��һ�㣬��O��BC�ཻ��F��G���㣬����AB��AC�ֱ������ڵ�D��E��DE��BC������DF��EG��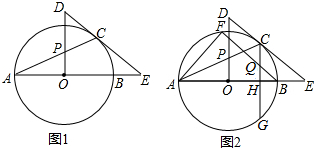
 ��ͼ���Գ���Ϊֱ��x=$\frac{7}{2}$�������߾�����A��6��0����B��0��-4����
��ͼ���Գ���Ϊֱ��x=$\frac{7}{2}$�������߾�����A��6��0����B��0��-4���� ��ͼ����a��b����1=60�㣬���2�Ķ���Ϊ120�ȣ�
��ͼ����a��b����1=60�㣬���2�Ķ���Ϊ120�ȣ�