题目内容
8. 如图,△ABC是边长为1的正三角形,弧AB和弧AC所对的圆心角均为120°,则图中阴影部分的面积为$\frac{\sqrt{3}}{12}$.
如图,△ABC是边长为1的正三角形,弧AB和弧AC所对的圆心角均为120°,则图中阴影部分的面积为$\frac{\sqrt{3}}{12}$.
分析 设$\widehat{AB}$与$\widehat{AC}$相交于点O,连OA,OB,OC,线段OA将阴影的上方部分分成两个弓形,将这两个弓形分别按顺时针及逆时针方向绕点O旋转120°后,阴影部分便合并成△OBC,得到它的面积等于△ABC面积的三分之一,利用等边三角形的面积公式:$\frac{\sqrt{3}}{4}$×边长2,即可求得阴影部分的面积.
解答 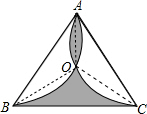 解:如图,设$\widehat{AB}$与$\widehat{AC}$相交于点O,连接OA,OB,OC,线段OA将阴影的上方部分分成两个弓形,将这两个弓形分别按顺时针及反时针绕点O旋转120°后,阴影部分便合并成△OBC,它的面积等于△ABC面积的三分之一,
解:如图,设$\widehat{AB}$与$\widehat{AC}$相交于点O,连接OA,OB,OC,线段OA将阴影的上方部分分成两个弓形,将这两个弓形分别按顺时针及反时针绕点O旋转120°后,阴影部分便合并成△OBC,它的面积等于△ABC面积的三分之一,
∴S阴影部分=$\frac{1}{3}$×$\frac{\sqrt{3}}{4}$×12=$\frac{\sqrt{3}}{12}$.
故答案为:$\frac{\sqrt{3}}{12}$.
点评 本题考查了旋转的性质:旋转前后两图形全等,对应点到旋转中心的距离相等,对应点与旋转中心的连线段所夹的角等于旋转角.也考查了等边三角形的面积公式:$\frac{\sqrt{3}}{4}$×边长2.

练习册系列答案
相关题目
19.2015年10月上市的某品牌手机经过连续两次降价,截至2016年3月底售价由原来的6500元/台,降至4200元/台.设平均每个季度的降价率为x,根据题意,可列出方程是( )
| A. | 4200(1+x)2=6500 | B. | 4200(1+2x)=6500 | C. | 6500(1-x)2=4200 | D. | 6500(1-2x)=4200 |
13.某小区要建一个地基为多边形的凉亭,如果这个多边形的外角和等于它的内角和,那么这个多边形是( )
| A. | 六边形 | B. | 五边形 | C. | 四边形 | D. | 三边形 |
17.下列图形既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
18.某商店通过调低价格的方式促销n个不同的玩具,调整后的单价y(元)与调整前的单价x(元)满足一次函数关系,如表:
已知这n个玩具调整后的单价都大于2元.
(1)求y与x的函数关系式,并确定x的取值范围;
(2)某个玩具调整前单价是108元,顾客购买这个玩具省了多少钱?
(3)这n个玩具调整前、后的平均单价分别为$\overline{x}$,$\overline{y}$,猜想$\overline{y}$与$\overline{x}$的关系式,并写出推导过程.
| 第1个 | 第2个 | 第3个 | 第4个 | … | 第n个 | |
| 调整前的单价x(元) | x1 | x2=6 | x3=72 | x4 | … | xn |
| 调整后的单价y(元) | y1 | y2=4 | y3=59 | y4 | … | yn |
(1)求y与x的函数关系式,并确定x的取值范围;
(2)某个玩具调整前单价是108元,顾客购买这个玩具省了多少钱?
(3)这n个玩具调整前、后的平均单价分别为$\overline{x}$,$\overline{y}$,猜想$\overline{y}$与$\overline{x}$的关系式,并写出推导过程.

 如图,在△ABC中,AB=AC,∠BAC=50?.分别以B、C为圆心,BC长为半径画弧,设两弧交于点D,与AB、AC的延长线分别交于点E、F,连接AD.则
如图,在△ABC中,AB=AC,∠BAC=50?.分别以B、C为圆心,BC长为半径画弧,设两弧交于点D,与AB、AC的延长线分别交于点E、F,连接AD.则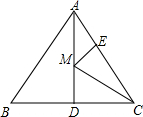 如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边的中点,则EM+CM的最小值为3$\sqrt{3}$.
如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边的中点,则EM+CM的最小值为3$\sqrt{3}$.