题目内容
7. 如图,对称轴为直线x=$\frac{7}{2}$的抛物线经过点A(6,0)和B(0,-4).
如图,对称轴为直线x=$\frac{7}{2}$的抛物线经过点A(6,0)和B(0,-4).(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第一象限,四边形OEAF是以OA为对角线的平行四边形,求平行四边形OEAF的面积S与x之间的函数关系式;
(3)当(2)中的平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形.
分析 (1)根据对称轴、A、B点的坐标,可得方程,根据解方程,可得答案;
(2)根据平行四边形的面积公式,可得函数解析式;
(3)根据函数值,可得E点坐标,根据菱形的判定,可得答案.
解答 解:(1)设抛物线的解析式为y=ax2+bx+c,
将A、B点的坐标代入函数解析式,得
$\left\{\begin{array}{l}{-\frac{b}{2a}=\frac{7}{2}}\\{36a+6b+c=0}\\{c=-4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{2}{3}}\\{b=\frac{14}{3}}\\{c=-4}\end{array}\right.$,
抛物线的解析式为y=-$\frac{2}{3}$x2+$\frac{14}{3}$x-4,
配方,得
y=-$\frac{2}{3}$(x-$\frac{7}{2}$)2+$\frac{25}{6}$,
顶点坐标为($\frac{7}{2}$,$\frac{25}{6}$);
(2)E点坐标为(x,-$\frac{2}{3}$x2+$\frac{14}{3}$x-4),
S=2×$\frac{1}{2}$OA•yE=6(-$\frac{2}{3}$x2+$\frac{14}{3}$x-4)
即S=-4x2+28x-24;
(3)平行四边形OEAF的面积为24时,平行四边形OEAF可能为菱形,理由如下:
当平行四边形OEAF的面积为24时,即
-4x2+28x-24=24,
化简,得
x2-7x+12=0,解得x=3或4,
当x=3时,EO=EA,平行四边形OEAF为菱形.
当x=4时,EO≠EA,平行四边形OEAF不为菱形.
∴平行四边形OEAF的面积为24时,平行四边形OEAF可能为菱形.
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式,配方法求函数的顶点坐标;利用平行四边形性质是解题关键;利用方程的判别式是解题关键.

| A. |  | B. |  | C. |  | D. |  |
| 第1个 | 第2个 | 第3个 | 第4个 | … | 第n个 | |
| 调整前的单价x(元) | x1 | x2=6 | x3=72 | x4 | … | xn |
| 调整后的单价y(元) | y1 | y2=4 | y3=59 | y4 | … | yn |
(1)求y与x的函数关系式,并确定x的取值范围;
(2)某个玩具调整前单价是108元,顾客购买这个玩具省了多少钱?
(3)这n个玩具调整前、后的平均单价分别为$\overline{x}$,$\overline{y}$,猜想$\overline{y}$与$\overline{x}$的关系式,并写出推导过程.

| A. | 5 | B. | 7 | C. | 8 | D. | $\frac{13}{2}$ |
| A. | 20(1+2x)=28.8 | B. | 28.8(1+x)2=20 | ||
| C. | 20(1+x)2=28.8 | D. | 20+20(1+x)+20(1+x)2=28.8 |
| A. | 4 | B. | 3.2 | C. | 3 | D. | 2 |
 如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OD⊥AB于点O,分别交AC、CF于点E、D,且DE=DC.
如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OD⊥AB于点O,分别交AC、CF于点E、D,且DE=DC.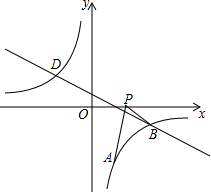 如图,已知点A(1,a)是反比例函数y=-$\frac{3}{x}$的图象上一点,直线y=-$\frac{1}{2}x+\frac{1}{2}$与反比例函数y=-$\frac{3}{x}$的图象在第四象限的交点为点B.
如图,已知点A(1,a)是反比例函数y=-$\frac{3}{x}$的图象上一点,直线y=-$\frac{1}{2}x+\frac{1}{2}$与反比例函数y=-$\frac{3}{x}$的图象在第四象限的交点为点B.