题目内容
9.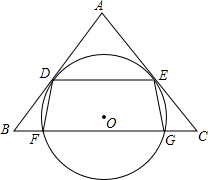 如图,O是△ABC内一点,⊙O与BC相交于F、G两点,且与AB、AC分别相切于点D、E,DE∥BC,连接DF、EG.
如图,O是△ABC内一点,⊙O与BC相交于F、G两点,且与AB、AC分别相切于点D、E,DE∥BC,连接DF、EG.(1)求证:AB=AC.
(2)已知AB=10,BC=12,求四边形DFGE是矩形时⊙O的半径.
分析 (1)由切线长定理可知AD=AE,易得∠ADE=∠AED,因为DE∥BC,由平行线的性质得∠ADE=∠B,∠AED=∠C,可得∠B=∠C,易得AB=AC;
(2)如图,连接AO,交DE于点M,延长AO交BC于点N,连接OE、DG,设⊙O半径为r,由△AOD∽△ABN得$\frac{OD}{BN}$=$\frac{AD}{AN}$,得到AD=$\frac{4}{3}$r,再由△GBD∽△ABN得$\frac{BD}{BN}$=$\frac{GD}{AN}$,列出方程即可解决问题.
解答 (1)证明:∵AD、AE是⊙O的切线,
∴AD=AE,
∴∠ADE=∠AED,
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴∠B=∠C,
∴AB=AC;
(2)解:如图,连接AO,交DE于点M,延长AO交BC于点N,连接OE、DG,设⊙O半径为r,
∵四边形DFGE是矩形,
∴∠DFG=90°,
∴DG是⊙O直径,
∵⊙O与AB、AC分别相切于点D、E,
∴OD⊥AB,OE⊥AC,
∵OD=OE,OE⊥AC,
∵OD=OE.
∴AN平分∠BAC,∵AB=AC,
∴AN⊥BC,BN=$\frac{1}{2}$BC=6,
在RT△ABN中,AN=$\sqrt{A{B}^{2}-B{N}^{2}}$=$\sqrt{1{0}^{2}-{6}^{2}}$=8,
∵OD⊥AB,AN⊥BC,
∴∠ADO=∠ANB=90°,
∵∠OAD=∠BAN,
∴△AOD∽△ABN,
∴$\frac{OD}{BN}$=$\frac{AD}{AN}$,即$\frac{r}{6}$=$\frac{AD}{8}$,
∴AD=$\frac{4}{3}$r,
∴BD=AB-AD=10-$\frac{4}{3}$r,
∵OD⊥AB,
∴∠GDB=∠ANB=90°,
∵∠B=∠B,
∴△GBD∽△ABN,
∴$\frac{BD}{BN}$=$\frac{GD}{AN}$,即$\frac{10-\frac{4}{3}r}{6}$=$\frac{2r}{8}$,
∴r=$\frac{60}{17}$,
∴四边形DFGE是矩形时⊙O的半径为$\frac{60}{17}$.
点评 本题考查圆、切线的性质、矩形的性质、相似三角形的判定和性质、勾股定理等知识,解题的关键是利用参数解决问题,学会用方程的思想思考问题,属于中考压轴题.

| A. | 4200(1+x)2=6500 | B. | 4200(1+2x)=6500 | C. | 6500(1-x)2=4200 | D. | 6500(1-2x)=4200 |
| A. |  | B. |  | C. |  | D. |  |
| A. | 1 | B. | -1 | C. | -5 | D. | 5 |
| A. | 200(1+a%)2=148 | B. | 200(1-a%)2=148 | C. | 200(1-2a%)=148 | D. | 200(1-a2%)=148 |
| A. | c<3 | B. | m≤$\frac{1}{2}$ | C. | n≤2 | D. | b<1 |
| 第1个 | 第2个 | 第3个 | 第4个 | … | 第n个 | |
| 调整前的单价x(元) | x1 | x2=6 | x3=72 | x4 | … | xn |
| 调整后的单价y(元) | y1 | y2=4 | y3=59 | y4 | … | yn |
(1)求y与x的函数关系式,并确定x的取值范围;
(2)某个玩具调整前单价是108元,顾客购买这个玩具省了多少钱?
(3)这n个玩具调整前、后的平均单价分别为$\overline{x}$,$\overline{y}$,猜想$\overline{y}$与$\overline{x}$的关系式,并写出推导过程.
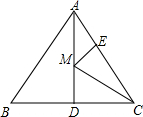 如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边的中点,则EM+CM的最小值为3$\sqrt{3}$.
如图,等边△ABC的边长为6,AD是BC边上的中线,M是AD上的动点,E是AC边的中点,则EM+CM的最小值为3$\sqrt{3}$.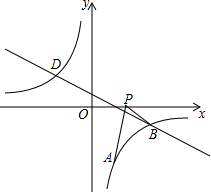 如图,已知点A(1,a)是反比例函数y=-$\frac{3}{x}$的图象上一点,直线y=-$\frac{1}{2}x+\frac{1}{2}$与反比例函数y=-$\frac{3}{x}$的图象在第四象限的交点为点B.
如图,已知点A(1,a)是反比例函数y=-$\frac{3}{x}$的图象上一点,直线y=-$\frac{1}{2}x+\frac{1}{2}$与反比例函数y=-$\frac{3}{x}$的图象在第四象限的交点为点B.