题目内容
13.已知一次函数y1=x+b(b为常数)的图象与反比例函数y2=$\frac{k}{x}$(k为常数,且k≠0)的图象相交于点P(3,1).(1)求这两个函数的解析式;
(2)若y1>y2,请直接写出x的取值范围.
分析 (1)由点P的坐标结合反比例函数图象上点的坐标特征可得出反比例函数系数k,由此即可得出反比例函数解析式;由点P的坐标利用待定系数法即可求出一次函数解析式;
(2)联立两函数解析式,求出两函数交点坐标,画出图形,根据函数图象的上下位置关系即可得出结论.
解答 解:(1)∵点P(3,1)在反比例函数图象上,
∴k=3×1=3,
∴反比例函数解析式为y2=$\frac{3}{x}$;
将点P(3,1)代入y1=x+b中,
得:1=3+b,解得:b=-2,
∴一次函数解析式为y1=x-2.
(2)联立两函数解析式得:$\left\{\begin{array}{l}{y=x-2}\\{y=\frac{3}{x}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-1}\\{y=-3}\end{array}\right.$或$\left\{\begin{array}{l}{x=3}\\{y=1}\end{array}\right.$,
∴一次函数y1=x-2与反比例函数y2=$\frac{3}{x}$的交点坐标为(-1,-3)和(3,1).
依照题意画出图形,如下所示.
观察函数图形,发现:
当-1<x<0或x>3时,一次函数图象在反比例函数图象上方,
∴当y1>y2时,x的取值范围为-1<x<0或x>3.
点评 本题考查了反比例函数与一次函数的交点问题、反比例函数图象上点的坐标特征以及待定系数法求函数解析式,解题的关键:(1)利用待定系数法求出函数解析式;(2)画出函数图象,利用数形结合解决问题.本题属于基础题,难度不大,解决该题型题目是,联立两函数解析式得出方程组,通过解方程组找出交点坐标,画出函数图象,利用数形结合解决问题是关键.

练习册系列答案
 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
4.计算(-2)+(-3)的值是( )
| A. | 1 | B. | -1 | C. | -5 | D. | 5 |
1.已知二次函数y=ax2+bx+c(a>0)的图象经过点A(-1,2),B(2,5),顶点坐标为(m,n),则下列说法错误的是( )
| A. | c<3 | B. | m≤$\frac{1}{2}$ | C. | n≤2 | D. | b<1 |
18.某商店通过调低价格的方式促销n个不同的玩具,调整后的单价y(元)与调整前的单价x(元)满足一次函数关系,如表:
已知这n个玩具调整后的单价都大于2元.
(1)求y与x的函数关系式,并确定x的取值范围;
(2)某个玩具调整前单价是108元,顾客购买这个玩具省了多少钱?
(3)这n个玩具调整前、后的平均单价分别为$\overline{x}$,$\overline{y}$,猜想$\overline{y}$与$\overline{x}$的关系式,并写出推导过程.
| 第1个 | 第2个 | 第3个 | 第4个 | … | 第n个 | |
| 调整前的单价x(元) | x1 | x2=6 | x3=72 | x4 | … | xn |
| 调整后的单价y(元) | y1 | y2=4 | y3=59 | y4 | … | yn |
(1)求y与x的函数关系式,并确定x的取值范围;
(2)某个玩具调整前单价是108元,顾客购买这个玩具省了多少钱?
(3)这n个玩具调整前、后的平均单价分别为$\overline{x}$,$\overline{y}$,猜想$\overline{y}$与$\overline{x}$的关系式,并写出推导过程.
 如图,在△ABC中,AB=AC,∠BAC=50?.分别以B、C为圆心,BC长为半径画弧,设两弧交于点D,与AB、AC的延长线分别交于点E、F,连接AD.则
如图,在△ABC中,AB=AC,∠BAC=50?.分别以B、C为圆心,BC长为半径画弧,设两弧交于点D,与AB、AC的延长线分别交于点E、F,连接AD.则

 如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OD⊥AB于点O,分别交AC、CF于点E、D,且DE=DC.
如图,△ABC是⊙O的内接三角形,AB是⊙O的直径,OD⊥AB于点O,分别交AC、CF于点E、D,且DE=DC.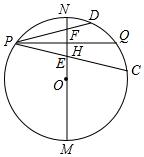 我们知道:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.你可以利用这一结论解决问题:
我们知道:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;平分弧的直径垂直平分这条弧所对的弦.你可以利用这一结论解决问题: