题目内容
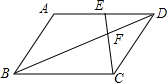
5. 如图,在?ABCD中,点E在CD边上,AB=3CE,射线AE交BC边的延长线于点F,则下列结论中错误的是( )
如图,在?ABCD中,点E在CD边上,AB=3CE,射线AE交BC边的延长线于点F,则下列结论中错误的是( )| A. | BF=3CF | B. | DE=2CE | C. | AE=2EF | D. | AD=3CF |
分析 根据平行四边形的性质可得AB∥CD,然后可得△ECF∽△ABF,再根据相似三角形的性质可得A结论正确;根据平行四边形的性质可得CD=AB,再由条件AB=3CE可得CD=3CE,根据线段的和差关系可得B结论正确;根据平行四边形的性质可得AB∥CD,进而可判定△ECF∽△ABF,根据相似三角形的性质可证出结论,进而可得C结论正确;根据平行四边形的性质可得AD∥CB,进而可得△ADE∽△FCE,再根据相似三角形的性质可得结论,从而可得D结论错误.
解答 解:A、∵四边形ABCD是平行四边形,
∴AB∥CD,
∴△ECF∽△ABF,
∴$\frac{CF}{BF}$=$\frac{CE}{AB}$,
∵AB=3CE,
∴BF=3CF,故A结论正确;
B、∵四边形ABCD是平行四边形,
∴CD=AB,
∵AB=3CE,
∴CD=3CE,
∴DE=2CE,故B结论正确;
C、∵四边形ABCD是平行四边形,
∴AB∥CD,
∴△ECF∽△ABF,
∴$\frac{EF}{AF}$=$\frac{CE}{AB}$,
∵AB=3CE,
∴AF=3EF,
∴AE=2EF,故C结论正确;
D、∵四边形ABCD是平行四边形,
∴AD∥CB,
∴△ADE∽△FCE,
∴$\frac{AD}{CF}$=$\frac{DE}{CE}$,
∵DE=2CE,
∴AD=2CF,故D结论错误;
故选:D.
点评 此题主要考查了平行四边形的性质,以及相似三角形的判定和性质,关键是掌握平行四边形对边平行且相等.

练习册系列答案
相关题目
13. 如图,在?ABCD中,点E在AD边上,EC交BD于点F,若BF=2DF,则下列结论错误的是( )
如图,在?ABCD中,点E在AD边上,EC交BD于点F,若BF=2DF,则下列结论错误的是( )
 如图,在?ABCD中,点E在AD边上,EC交BD于点F,若BF=2DF,则下列结论错误的是( )
如图,在?ABCD中,点E在AD边上,EC交BD于点F,若BF=2DF,则下列结论错误的是( )| A. | CF=2EF | B. | BC=2AE | C. | CE=2EF | D. | AE=ED |
20.某物品原价为160元,连续两次降价α%后售价为128元,下列所列方程正确的是( )
| A. | (1+a%)2=$\frac{128}{160}$ | B. | (1-a%)2=$\frac{128}{160}$ | C. | (1-2a%)=$\frac{128}{160}$ | D. | (1-a%)=$\frac{128}{160}$ |
14.下列语句中不是命题的是( )
| A. | 等角的余角相等 | B. | 过一点作已知直线的垂线 | ||
| C. | 对顶角相等 | D. | 两直线平行,同位角相等 |
 如图,已知△ABC的三边长为别为5,12,13,分别以三边为直径向上作三个半圆,求图中阴影部分的面积.
如图,已知△ABC的三边长为别为5,12,13,分别以三边为直径向上作三个半圆,求图中阴影部分的面积.