题目内容
13.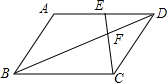 如图,在?ABCD中,点E在AD边上,EC交BD于点F,若BF=2DF,则下列结论错误的是( )
如图,在?ABCD中,点E在AD边上,EC交BD于点F,若BF=2DF,则下列结论错误的是( )| A. | CF=2EF | B. | BC=2AE | C. | CE=2EF | D. | AE=ED |
分析 由平行四边形的性质得出AD∥BC,AD=BC,证出△BCF∽△DEF,得出对应边成比例$\frac{CF}{EF}=\frac{BC}{DE}=\frac{BF}{DF}$=2,即可得出结论.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∴△BCF∽△DEF,
∴$\frac{CF}{EF}=\frac{BC}{DE}=\frac{BF}{DF}$=2,
∴CF=2EF,BC=2DE,
∴BC=2DE=2AE,AE=ED,CE=3EF,
∴选项A、B、D正确,选项C错误;
故选:C.
点评 本题考查了平行四边形的性质、相似三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形相似是解决问题的关键.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
4.?ABCD中∠A为50°,则∠B为( )度.
| A. | 50 | B. | 40 | C. | 130 | D. | 150 |
8.某商店出售一种商品,若每件10元,则每天可销售50件,售价每降低1元,可多买6件,要使该商品每天的销售额(总售价)为504元,设每件降低x元,则可列方程为( )
| A. | (50+x)(10-x)=504 | B. | 50(10-x)=504 | C. | (10-x)(50+6x)=504 | D. | (10-6x)(50+x)=504 |
5. 如图,在?ABCD中,点E在CD边上,AB=3CE,射线AE交BC边的延长线于点F,则下列结论中错误的是( )
如图,在?ABCD中,点E在CD边上,AB=3CE,射线AE交BC边的延长线于点F,则下列结论中错误的是( )
 如图,在?ABCD中,点E在CD边上,AB=3CE,射线AE交BC边的延长线于点F,则下列结论中错误的是( )
如图,在?ABCD中,点E在CD边上,AB=3CE,射线AE交BC边的延长线于点F,则下列结论中错误的是( )| A. | BF=3CF | B. | DE=2CE | C. | AE=2EF | D. | AD=3CF |
3.下列各式由左边到右边的变形中,是因式分解的是( )
| A. | 3(a+b)=3a+3b | B. | x2+6x+9=x(x+6)+9 | C. | a2-2=(a+2)(a-2) | D. | ax-ay=a(x-y) |
 一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另外有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图所示).
一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另外有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图所示). 如图,四边形ABCD是⊙O的内接四边形,∠B=135°,则∠AOC的度数为90°.
如图,四边形ABCD是⊙O的内接四边形,∠B=135°,则∠AOC的度数为90°.