题目内容
10.阅读下列材料,解答相应问题:数学知识伴随着人类文明的起源而产生,人类祖先为我们留下了许多珍贵的原始资料,和古巴比伦楔形文字泥板书,古巴比伦泥板上记载了两种利用平方数表计算两数乘积的公式:
ab=$\frac{1}{4}$[(a+b)2-(a-b)2]…①
ab=$\frac{1}{2}$[(a+b)2-a2-b2]…②
(1)补全材料中公式②中的空缺部分;
(2)验证材料中的公式①;
(3)当a+b=5,a-b=7时,利用公式①计算ab的值.
分析 (1)利用完全平方公式将(a+b)2展开,留下含ab的项,即可得出结论;
(2)利用完全平方公式将(a+b)2和(a-b)2展开,合并同类项后即可得出公式右边=ab=公式左边,由此即可证出公式成立;
(3)将a+b=5,a-b=7代入公式①中,即可求出ab的值.
解答 解:(1)∵(a+b)2=a2+b2+2ab,
∴ab=$\frac{1}{2}$[(a+b)2-a2-b2].
故答案为:-b2.
(2)公式①的右边=$\frac{1}{4}$[a2+b2+2ab-(a2+b2-2ab)],
=$\frac{1}{4}$[a2+b2+2ab-a2-b2+2ab],
=$\frac{1}{4}$×4ab,
=ab.
因为公式①的左边=ab,
所以公式①左边=右边,公式成立.
(3)把a+b=5,a-b=7代入公式①,
得:ab=$\frac{1}{4}$×(52-72),
=$\frac{1}{4}$×(-24),
=-6.
点评 本题考查了完全平方公式,解题的关键是:(1)根据完全平方公式的展开式将公式②补充完整;(2)利用完全平方公式的展开式将公式①的右边进行变形,从而得出结论成立;(3)套用公式①代入数据求值.本题属于基础题,难度不大,解决该题型题目时,熟练掌握完全平方公式的应用是关键.

练习册系列答案
相关题目
5. 如图,在?ABCD中,点E在CD边上,AB=3CE,射线AE交BC边的延长线于点F,则下列结论中错误的是( )
如图,在?ABCD中,点E在CD边上,AB=3CE,射线AE交BC边的延长线于点F,则下列结论中错误的是( )
 如图,在?ABCD中,点E在CD边上,AB=3CE,射线AE交BC边的延长线于点F,则下列结论中错误的是( )
如图,在?ABCD中,点E在CD边上,AB=3CE,射线AE交BC边的延长线于点F,则下列结论中错误的是( )| A. | BF=3CF | B. | DE=2CE | C. | AE=2EF | D. | AD=3CF |
19.下列的三条线段能组成三角形的是( )
| A. | 1,2,3 | B. | 2,2,4 | C. | 3,4,5 | D. | 3,4,8 |
 如图,四边形ABCD是⊙O的内接四边形,∠B=135°,则∠AOC的度数为90°.
如图,四边形ABCD是⊙O的内接四边形,∠B=135°,则∠AOC的度数为90°.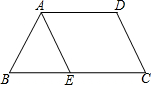 如图,已知梯形ABCD中,AD∥BC,点E在BC边上,AE∥DC,DC=AB.如果图中的线段都是有向线段,则与$\overrightarrow{AE}$相等的向量是$\overrightarrow{DC}$.
如图,已知梯形ABCD中,AD∥BC,点E在BC边上,AE∥DC,DC=AB.如果图中的线段都是有向线段,则与$\overrightarrow{AE}$相等的向量是$\overrightarrow{DC}$. 如图:AB∥DE,∠1=∠2,AC平分∠BAD,试说明AD∥BC.
如图:AB∥DE,∠1=∠2,AC平分∠BAD,试说明AD∥BC.