题目内容
18.函数y=x2-2x-3,当y<0时,x的取值范围为-1<x<3;当-1<x<2时,y的取值范围为-4<y<0.分析 根据函数解析式可以确定图象与x轴的交点是(-1,0),(3,0),又当y<0时,图象在x轴的下方,由此可以确定x的取值范围,结合函数解析式求出y的取值范围.
解答 解:当y=0时,即x2-2x-3=0,
∴x1=-1,x2=3,
∴图象与x轴的交点是(-1,0),(3,0),
当y<0时,图象在x轴的下方,
此时-1<x<3.
当-1<x<2时,y的取值范围为:-4<y<0,
故答案为:-1<x<3,-4<y<0.
点评 本题主要考查了抛物线与x轴的交点问题,解答此题的关键是求出图象与x轴的交点,然后由图象找出当y<0时,自变量x的范围,锻炼了学生数形结合的思想方法.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
13.已知抛物线y=-(x+1)2+m经过点A(0,3),它的解析式为( )
| A. | y=-(x-1)2+4 | B. | y=-(x+1)2+3 | C. | y=-(x+1)2-3 | D. | y=-(x+1)2+4 |
 已知:在Rt△ABD中,∠ABD=90°,以直角边AB为直径作圆O交AD于C,取线段BD的中点E,连接CE交AB的延长线于P.
已知:在Rt△ABD中,∠ABD=90°,以直角边AB为直径作圆O交AD于C,取线段BD的中点E,连接CE交AB的延长线于P. 阅读:|5-2|表示5与2差的绝对值,也可理解为5与2两位数在数轴上所对应的两点之间的距离;|5+2|可以看做|5-(-2)|,表示5与-2的差的绝对值,也可理解为5与-2两位数在数轴上所对应的两点之间的距离,探索:
阅读:|5-2|表示5与2差的绝对值,也可理解为5与2两位数在数轴上所对应的两点之间的距离;|5+2|可以看做|5-(-2)|,表示5与-2的差的绝对值,也可理解为5与-2两位数在数轴上所对应的两点之间的距离,探索: 如图△ABC中,tan∠C=$\frac{1}{2}$,DE⊥AC,若CE=5,DE=1,且△BEC的面积是△ADE面积的10倍,则BE的长度是$\sqrt{5}$.
如图△ABC中,tan∠C=$\frac{1}{2}$,DE⊥AC,若CE=5,DE=1,且△BEC的面积是△ADE面积的10倍,则BE的长度是$\sqrt{5}$. 如图所示,在△ABC中,AB=CB,∠ABC=90°,∠CAB=∠ACB,F为AB延长线上一点,点E在BC上,且∠EAB=∠FCB.
如图所示,在△ABC中,AB=CB,∠ABC=90°,∠CAB=∠ACB,F为AB延长线上一点,点E在BC上,且∠EAB=∠FCB.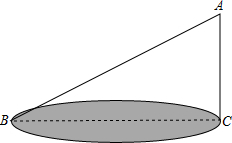 公园有三个景点A、B、C构成如图所示的直角三角形,由于B、C两景点之间有一山相隔,为方便游客,准备在B、C间挖条隧道.已知∠ACB=90°,AB=3千米,AC=2千米.试用计算器探索:这条隧道至少要修多少米?(精确到1米)
公园有三个景点A、B、C构成如图所示的直角三角形,由于B、C两景点之间有一山相隔,为方便游客,准备在B、C间挖条隧道.已知∠ACB=90°,AB=3千米,AC=2千米.试用计算器探索:这条隧道至少要修多少米?(精确到1米) 如图,有一张边长为6的正方形纸片ABCD,P是AD边上一点(不与点A、D重合),将正方形纸片沿EF折叠,使点B落在点P处,点C落在点G处,PG交DC于H,连接BP.
如图,有一张边长为6的正方形纸片ABCD,P是AD边上一点(不与点A、D重合),将正方形纸片沿EF折叠,使点B落在点P处,点C落在点G处,PG交DC于H,连接BP.