题目内容
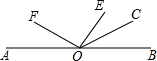 如图,点O为直线AB上的一点,OE,OF,OC是射线,OE⊥OF.若∠BOC=2∠COE,∠AOF=48°,求∠EOC的度数为
如图,点O为直线AB上的一点,OE,OF,OC是射线,OE⊥OF.若∠BOC=2∠COE,∠AOF=48°,求∠EOC的度数为考点:垂线,角的计算
专题:
分析:根据垂线的定义,可得∠EOF的度数,根据角的和差,可得∠BOE的度数,根据∠BOC=2∠COE,可得关于∠COE的方程,根据解方程,可得答案.
解答:解:由OE⊥OF,∠EOF=90°.
由角的和差,得
∠BOE=180°-∠A0F-∠EOF=180°-48°-90°=42°.
由∠BOC=2∠COE,角的和差,得
∠BOE=∠EOC+∠BOC=∠EOC+2∠EOC=3∠EOC=42°.
解得∠EOC=14°,
故答案为:14°.
由角的和差,得
∠BOE=180°-∠A0F-∠EOF=180°-48°-90°=42°.
由∠BOC=2∠COE,角的和差,得
∠BOE=∠EOC+∠BOC=∠EOC+2∠EOC=3∠EOC=42°.
解得∠EOC=14°,
故答案为:14°.
点评:本题考查了垂线,两线垂直时所成的角是90°,利用了三个角的和是平角.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
点A(-5,-y1)、B(-2,-y2)都在直线y=-3x+5上,则y1与y2的关系是( )
| A、y1≤y2 |
| B、y1=y2 |
| C、y1>y2 |
| D、y1<y2 |
 如图所示,点C在以AB为直径的⊙O上,CD⊥AB于点P.求当AP=
如图所示,点C在以AB为直径的⊙O上,CD⊥AB于点P.求当AP= 如图,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=8,ON,CD分别为两圆的半径,求阴影部分的面积.
如图,在两个半圆中,大圆的弦MN与小圆相切,D为切点,且MN∥AB,MN=8,ON,CD分别为两圆的半径,求阴影部分的面积. 如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.
如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.