题目内容
(1)O是△ABC的内心,∠BOC=130°,则∠A= .
(2)一个三角形的外心与内心恰好重合,这个三角形是 .
(2)一个三角形的外心与内心恰好重合,这个三角形是
考点:三角形的内切圆与内心
专题:
分析:(1)根据三角形内角和定理求出∠OBC+∠OCB=50°,根据角平分线定义求出∠ABC+∠ACB,根据三角形的内角和定理求出即可;
(2)根据等边三角形的性质得出三边相等,根据等腰三角形的性质得出即可.
(2)根据等边三角形的性质得出三边相等,根据等腰三角形的性质得出即可.
解答:解:(1)
∵∠BOC=130°,
∴∠OBC+∠OCB=180°-130°=50°,
∵O是△ABC的内心,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴∠ABC+∠ACB=2×50°=100°,
∴∠A=180°-(∠ABC+∠ACB)=80°,
故答案为:80°;
(2)一个三角形的外心与内心恰好重合,这个三角形是等边三角形,
故答案为:等边三角形.

∵∠BOC=130°,
∴∠OBC+∠OCB=180°-130°=50°,
∵O是△ABC的内心,
∴∠ABC=2∠OBC,∠ACB=2∠OCB,
∴∠ABC+∠ACB=2×50°=100°,
∴∠A=180°-(∠ABC+∠ACB)=80°,
故答案为:80°;
(2)一个三角形的外心与内心恰好重合,这个三角形是等边三角形,
故答案为:等边三角形.
点评:本题考查了三角形的内心和内切圆,等边三角形的性质,等腰三角形的性质的应用,能熟练地运用性质进行推理是解此题的关键.

练习册系列答案
相关题目
 如图,△ABC是等边三角形,D是BC上一点,AB=8,BD=3,将△ABD饶点A逆时针旋转60°到△ACE的位置,连接DE,则DE的长为
如图,△ABC是等边三角形,D是BC上一点,AB=8,BD=3,将△ABD饶点A逆时针旋转60°到△ACE的位置,连接DE,则DE的长为 在同一条公路旁,住着五个人,他们在同一家公司上班,如图所示,不妨设这五个人的家分别住在点A,B,D,E,F的位置,公司在点C,若AB=4km,BC=2km,CD=3km,DE=3km,EF=1km,他们全部乘出租车上班,车费单位报销,出租车收费标准是:起步价3元(3km以内,包括3km)以后每千米1.5元(不足1km,以1km计算),每辆车能容纳3人.
在同一条公路旁,住着五个人,他们在同一家公司上班,如图所示,不妨设这五个人的家分别住在点A,B,D,E,F的位置,公司在点C,若AB=4km,BC=2km,CD=3km,DE=3km,EF=1km,他们全部乘出租车上班,车费单位报销,出租车收费标准是:起步价3元(3km以内,包括3km)以后每千米1.5元(不足1km,以1km计算),每辆车能容纳3人.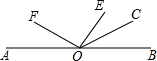 如图,点O为直线AB上的一点,OE,OF,OC是射线,OE⊥OF.若∠BOC=2∠COE,∠AOF=48°,求∠EOC的度数为
如图,点O为直线AB上的一点,OE,OF,OC是射线,OE⊥OF.若∠BOC=2∠COE,∠AOF=48°,求∠EOC的度数为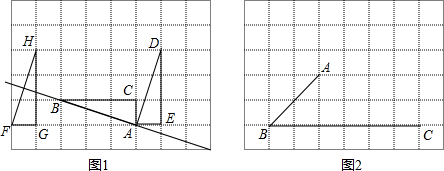
 如图,在△ABC中,∠BAC=60°,在△ABC的内部取一点O,连接OA,OB,OC,恰有OA=OC,∠OBA=20°,∠OCA=40°.①∠BOA=140°;②△OAB是等腰三角形;③∠OBC=30°;④△OBC是等腰三角形;⑤△ABC是等边三角形,则以上说法中正确的是( )
如图,在△ABC中,∠BAC=60°,在△ABC的内部取一点O,连接OA,OB,OC,恰有OA=OC,∠OBA=20°,∠OCA=40°.①∠BOA=140°;②△OAB是等腰三角形;③∠OBC=30°;④△OBC是等腰三角形;⑤△ABC是等边三角形,则以上说法中正确的是( ) 2012年,合肥市积极创建“全国文明城市”,某学生将“创建文明城市”写在正方体的六个面上,如图是该正方体的展开图,将它折叠成正方体后“创”字的对面是( )
2012年,合肥市积极创建“全国文明城市”,某学生将“创建文明城市”写在正方体的六个面上,如图是该正方体的展开图,将它折叠成正方体后“创”字的对面是( )