题目内容
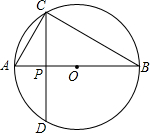 如图所示,点C在以AB为直径的⊙O上,CD⊥AB于点P.求当AP=
如图所示,点C在以AB为直径的⊙O上,CD⊥AB于点P.求当AP=| 1 |
| 4 |
考点:垂径定理,含30度角的直角三角形,圆周角定理
专题:计算题
分析:根据垂径定理由CD⊥AB得到
=
,根据圆周角定理得∠ACP=∠B,于是可判断Rt△CAP∽Rt△BCP,利用相似比得CP2=AP•PB,再由AP=
AB得到PA=
PB,所以CP2=
PB•PB,解得CP=
PB,然后在Rt△BCP中利用∠B的正切求出∠B的度数.
 |
| AC |
 |
| AD |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
解答:解:∵CD⊥AB,
∴
=
,
∴∠ACP=∠B,
∴Rt△CAP∽Rt△BCP,
∴
=
,
∴CP2=AP•PB,
∵AP=
AB,
∴PA=
PB,
∴CP2=
PB•PB,解得CP=
PB,
在Rt△BCP中,∵tanB=
=
,
∴∠B=30°.
∴
 |
| AC |
 |
| AD |
∴∠ACP=∠B,
∴Rt△CAP∽Rt△BCP,
∴
| CP |
| PB |
| AP |
| CP |
∴CP2=AP•PB,
∵AP=
| 1 |
| 4 |
∴PA=
| 1 |
| 3 |
∴CP2=
| 1 |
| 3 |
| ||
| 3 |
在Rt△BCP中,∵tanB=
| CP |
| PB |
| ||
| 3 |
∴∠B=30°.
点评:本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了锐角三角函数的定义和圆周角定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
实数a、b在数轴上分别对应A、B两点,A点在原点左侧,B点在原点右侧,且|a|<|b|,则
的值是( )
| a-b |
| a+b |
| A、大于0 | B、小于0 |
| C、等于0 | D、不能确定 |
在Rt△ABC中,∠A、∠B.∠C对边分别为a、b、c,∠C=90°,若sinA=
,则cosB=( )
| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
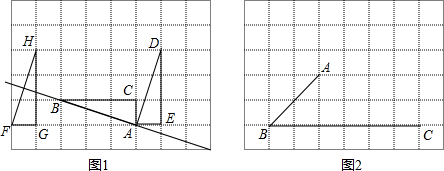
 如图,△ABC是等边三角形,D是BC上一点,AB=8,BD=3,将△ABD饶点A逆时针旋转60°到△ACE的位置,连接DE,则DE的长为
如图,△ABC是等边三角形,D是BC上一点,AB=8,BD=3,将△ABD饶点A逆时针旋转60°到△ACE的位置,连接DE,则DE的长为 在同一条公路旁,住着五个人,他们在同一家公司上班,如图所示,不妨设这五个人的家分别住在点A,B,D,E,F的位置,公司在点C,若AB=4km,BC=2km,CD=3km,DE=3km,EF=1km,他们全部乘出租车上班,车费单位报销,出租车收费标准是:起步价3元(3km以内,包括3km)以后每千米1.5元(不足1km,以1km计算),每辆车能容纳3人.
在同一条公路旁,住着五个人,他们在同一家公司上班,如图所示,不妨设这五个人的家分别住在点A,B,D,E,F的位置,公司在点C,若AB=4km,BC=2km,CD=3km,DE=3km,EF=1km,他们全部乘出租车上班,车费单位报销,出租车收费标准是:起步价3元(3km以内,包括3km)以后每千米1.5元(不足1km,以1km计算),每辆车能容纳3人.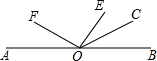 如图,点O为直线AB上的一点,OE,OF,OC是射线,OE⊥OF.若∠BOC=2∠COE,∠AOF=48°,求∠EOC的度数为
如图,点O为直线AB上的一点,OE,OF,OC是射线,OE⊥OF.若∠BOC=2∠COE,∠AOF=48°,求∠EOC的度数为