题目内容
 如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.
如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.(1)试说明△ABD≌△BCE;
(2)求∠AFE的度数.
考点:全等三角形的判定与性质,等边三角形的性质
专题:
分析:(1)根据等边三角形的性质可得到AB=BC,∠ABD=∠C,结合条件可证明△ABD≌△BCE;
(2)由(1)可得∠BAD=∠FBD,结合外角的性质可求得∠AFE.
(2)由(1)可得∠BAD=∠FBD,结合外角的性质可求得∠AFE.
解答:(1)证明:∵△ABC为等边三角形,
∴AB=BC,∠ABD=∠C=60°,
在△ABD和△BCE中
∴△ABD≌△BCE(SAS);
(2)解:由(1)有△ABD≌△BCE,
∴∠BAF=∠FBD,
∴∠AFE=∠BAF+∠ABF=∠ABF+∠FBD=∠ABD=60°.
∴AB=BC,∠ABD=∠C=60°,
在△ABD和△BCE中
|
∴△ABD≌△BCE(SAS);
(2)解:由(1)有△ABD≌△BCE,
∴∠BAF=∠FBD,
∴∠AFE=∠BAF+∠ABF=∠ABF+∠FBD=∠ABD=60°.
点评:本题主要考查等边三角形的性质和全等三角形的判定和性质,掌握等边三角形的三边、三个内角都相等是解题的关键,注意外角性质的利用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在Rt△ABC中,∠A、∠B.∠C对边分别为a、b、c,∠C=90°,若sinA=
,则cosB=( )
| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图中,边长k等于5的直角三角形有( )


| A、1个 | B、2个 | C、3个 | D、4个 |
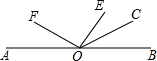 如图,点O为直线AB上的一点,OE,OF,OC是射线,OE⊥OF.若∠BOC=2∠COE,∠AOF=48°,求∠EOC的度数为
如图,点O为直线AB上的一点,OE,OF,OC是射线,OE⊥OF.若∠BOC=2∠COE,∠AOF=48°,求∠EOC的度数为 如图,数轴上A,B,C三点所表示的有理数的和是
如图,数轴上A,B,C三点所表示的有理数的和是 2012年,合肥市积极创建“全国文明城市”,某学生将“创建文明城市”写在正方体的六个面上,如图是该正方体的展开图,将它折叠成正方体后“创”字的对面是( )
2012年,合肥市积极创建“全国文明城市”,某学生将“创建文明城市”写在正方体的六个面上,如图是该正方体的展开图,将它折叠成正方体后“创”字的对面是( )