题目内容
如图,在平面直角坐标系中,抛物线 与
与 轴交与点
轴交与点 ,与
,与 轴交于
轴交于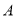 、
、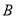 两点,点
两点,点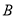 坐标为
坐标为 ,抛物线的对称轴方程为
,抛物线的对称轴方程为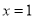 .
.
( )求抛物线的解析式.
)求抛物线的解析式.
( )点
)点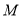 从
从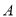 点出发,在线段
点出发,在线段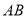 上以每秒
上以每秒 个单位长度的速度向
个单位长度的速度向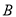 点运动,同时点
点运动,同时点 从
从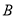 点出发,在线段
点出发,在线段 上以每秒
上以每秒 个单位长度的速度向
个单位长度的速度向 点运动,其中一个点到达终点时,另一个点也停止运动,在点
点运动,其中一个点到达终点时,另一个点也停止运动,在点 运动过程中,是否存在某一时刻
运动过程中,是否存在某一时刻 ,使
,使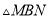 为直角三角形?若存在,求出
为直角三角形?若存在,求出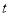 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
( )若点
)若点 为抛物线对称轴上一点,当
为抛物线对称轴上一点,当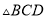 是直角三角形时,求点
是直角三角形时,求点 的坐标.
的坐标.
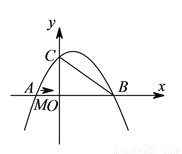
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


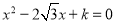 有两个相等的实数根,则k值为_____.
有两个相等的实数根,则k值为_____. )
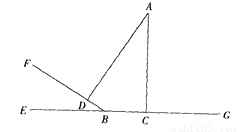
)
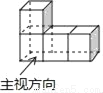
 B.
B.  C.
C.  D.
D. 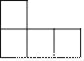
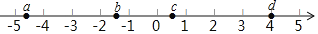
 ,求下列代数式的值:(
,求下列代数式的值:( )
) ;(
;( )
)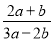 .
. ,
,  ,
,  ,
,  .将它们背面朝上洗匀后,从中随机抽取一张卡片,则其正面的数比
.将它们背面朝上洗匀后,从中随机抽取一张卡片,则其正面的数比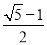 小的概率是__________.
小的概率是__________.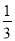 ,那么另一组数据3x1-2,3x2-2,3x3-2,3x4-2,3x 5-2的平均数是________,方差是________.
,那么另一组数据3x1-2,3x2-2,3x3-2,3x4-2,3x 5-2的平均数是________,方差是________.