题目内容
当-2≤x≤1,二次函数y=-(x-h)2+8的最大值为4,则实数h的值为 .
考点:二次函数的最值
专题:
分析:按照分类讨论的数学思想,分h<-2或h>1来分类解析,问题即可解决.
解答:解:∵二次函数y=-(x-h)2+8的最大值为4,
∴h<-2或h>1;
由二次函数的性质得:
当 x=-2或1时,y=4,
即-(-2-h)2+8=4①,或-(1-h)2+8=4②,
解①得h=0或-4;解②得h=3或-1,
∴h的值为-4或3.
∴h<-2或h>1;
由二次函数的性质得:
当 x=-2或1时,y=4,
即-(-2-h)2+8=4①,或-(1-h)2+8=4②,
解①得h=0或-4;解②得h=3或-1,
∴h的值为-4或3.
点评:该题主要考查了二次函数的性质及其应用问题;解题的关键是灵活运用二次函数的对称性及增减性来分析、判断、推理或解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,BE⊥CD,DF⊥BC,BE=DE,BC=10,CE=6,求AB的长.
如图,BE⊥CD,DF⊥BC,BE=DE,BC=10,CE=6,求AB的长.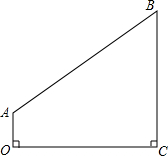 在四边形ABCO中,∠AOC=∠OCB=90°,AO=2,OC=8,CB=8
在四边形ABCO中,∠AOC=∠OCB=90°,AO=2,OC=8,CB=8 如图,Rt△BC中,∠BAC=90°,AD⊥BC于D,E是AC上任意一点,连接BE,过A作AF⊥BE于F,求证:BD•BC=BF•BE.
如图,Rt△BC中,∠BAC=90°,AD⊥BC于D,E是AC上任意一点,连接BE,过A作AF⊥BE于F,求证:BD•BC=BF•BE.