题目内容
已知抛物线y=4(x-k)2-9与x轴有两个交点,且都在原点的左侧,求k的取值范围.
考点:抛物线与x轴的交点
专题:
分析:首先设出抛物线y=4(x-k)2-9与x轴有两个交点,利用两个交点的范围,进一步建立抛物线与一元二次方程的关系,利用根与系数的关系建立不等式组,求得答案即可.
解答:解:设抛物线y=4(x-k)2-9与x轴交于(x1,0)(x2,0),则x1,x2是4(x-k)2-9=0的两根.
由已知得 x1<0,x2<0,
4(x-k)2-9=0,
即4x2-8kx+4k2-9=0,
,
解这个不等式组得-
<k<0.
由已知得 x1<0,x2<0,
4(x-k)2-9=0,
即4x2-8kx+4k2-9=0,
|
解这个不等式组得-
| 3 |
| 2 |
点评:此题考查抛物线与x轴的交点问题,利用二次函数与一元二次方程之间的联系,求得问题的答案.

练习册系列答案
相关题目
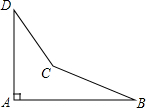 一个飞机零件的形状如图所示,按规定∠A应等于90°,∠B,∠D应分别是20°和30°,李师傅量得∠BCD=143°,就能断定这个零件不合格,你能说出其中的道理吗?
一个飞机零件的形状如图所示,按规定∠A应等于90°,∠B,∠D应分别是20°和30°,李师傅量得∠BCD=143°,就能断定这个零件不合格,你能说出其中的道理吗?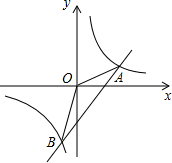 如图,双曲线:
如图,双曲线: 王师傅驾车到某地,汽车出发前油箱有油50升,行驶若干小时后,途中在加油站加油若干升,油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.
王师傅驾车到某地,汽车出发前油箱有油50升,行驶若干小时后,途中在加油站加油若干升,油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.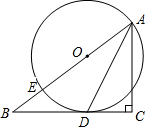 如图,O是 Rt△ABC的斜边AB上的一点,以O为中心、OA为半径的圆与BC相切于点D,与AB交于点E,∠DAO=28°,求∠DAC的度数.
如图,O是 Rt△ABC的斜边AB上的一点,以O为中心、OA为半径的圆与BC相切于点D,与AB交于点E,∠DAO=28°,求∠DAC的度数.