题目内容
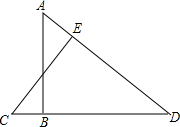
 如图,BE⊥CD,DF⊥BC,BE=DE,BC=10,CE=6,求AB的长.
如图,BE⊥CD,DF⊥BC,BE=DE,BC=10,CE=6,求AB的长.考点:全等三角形的判定与性质
专题:
分析:易证∠B=∠D,即可证明△BCE≌△DAE,可得CE=AE,根据勾股定理即可求得BE的长,即可解题.
解答:解:∵∠D+∠C=90°,∠C+∠B=90°,
∴∠B=∠D,
在△BCE和△DAE中,
,
∴△BCE≌△DAE(ASA),
∴AE=CE=6,
∵BE=
=8,
∴AB=BE-AE=2.
∴∠B=∠D,
在△BCE和△DAE中,
|
∴△BCE≌△DAE(ASA),
∴AE=CE=6,
∵BE=
| BC2-CE2 |
∴AB=BE-AE=2.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△BCE≌△DAE是解题的关键.

练习册系列答案
相关题目
 已知:如图,CE⊥AD,垂足为E,∠A=∠C,求证:AB⊥CD.
已知:如图,CE⊥AD,垂足为E,∠A=∠C,求证:AB⊥CD.