题目内容
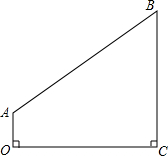 在四边形ABCO中,∠AOC=∠OCB=90°,AO=2,OC=8,CB=8
在四边形ABCO中,∠AOC=∠OCB=90°,AO=2,OC=8,CB=8(1)求线段AB长;
(2)点P为直线AO上一点,且△PAB为等腰三角形,则线段OP长为
考点:矩形的判定与性质,勾股定理,相似三角形的判定与性质
专题:
分析:(1)如图1,作辅助线,直接运用勾股定理来解答即可解决问题.
(2)如图2,作辅助线,按照分类讨论的数学思想,分AB为底或腰来逐一解析,问题即可解决.
(2)如图2,作辅助线,按照分类讨论的数学思想,分AB为底或腰来逐一解析,问题即可解决.
解答:解:(1)如图1,过点A作AD⊥BC,
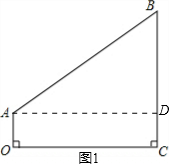
则四边形AOCD为矩形,
∴AD=OC=8,DC=AO=2,
∴BD=BC-CD=6;由勾股定理得:
AB2=AD2+BD2=64+36=100,
∴AB=10.
(2)如图2,点P在OA的延长线上,且AB为等腰△PAB的底,过P做PQ⊥AB于点Q;
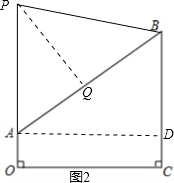
则AQ=BQ=
AB=5;
∵∠AOC=∠OCB=90°,
∴AO∥BC,∠PAQ=∠ABD,
∴△PAQ∽△ABD,
∴PA:AB=AQ:BD,而AB=10,AQ=5,BD=6,
∴PA=
,OP=2+
=
.
若AB为等腰△PAB的腰,则PA=AB或PB=AB;
若PA=AB,则:
①当点P在OA的延长线上时,
OP=10+2=12;
②当点P在AO的延长线上时,
OP=10-2=8;
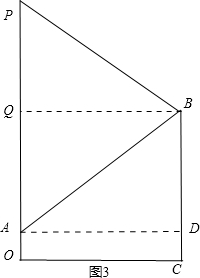
若PB=AB,如图3,过点B作BQ⊥PA,
则AQ=BQ;而四边形ADBQ为矩形,
∴AQ=BD=6,
∴OP=12+2=14,
故答案为
,8,12,14.

则四边形AOCD为矩形,
∴AD=OC=8,DC=AO=2,
∴BD=BC-CD=6;由勾股定理得:
AB2=AD2+BD2=64+36=100,
∴AB=10.
(2)如图2,点P在OA的延长线上,且AB为等腰△PAB的底,过P做PQ⊥AB于点Q;

则AQ=BQ=
| 1 |
| 2 |
∵∠AOC=∠OCB=90°,
∴AO∥BC,∠PAQ=∠ABD,
∴△PAQ∽△ABD,
∴PA:AB=AQ:BD,而AB=10,AQ=5,BD=6,
∴PA=
| 25 |
| 3 |
| 25 |
| 3 |
| 31 |
| 3 |
若AB为等腰△PAB的腰,则PA=AB或PB=AB;
若PA=AB,则:
①当点P在OA的延长线上时,
OP=10+2=12;
②当点P在AO的延长线上时,
OP=10-2=8;
若PB=AB,如图3,过点B作BQ⊥PA,
则AQ=BQ;而四边形ADBQ为矩形,
∴AQ=BD=6,
∴OP=12+2=14,
故答案为
| 31 |
| 3 |

点评:该题主要考查了勾股定理、相似三角形的判定及其性质、矩形的性质等几何知识点的应用问题;解题的关键是作辅助线,灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
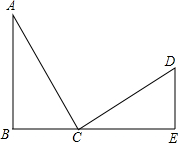 如图,∠B=∠E=90°,AB=CE,AC=CD,∠D=60°,CD=8cm.求:
如图,∠B=∠E=90°,AB=CE,AC=CD,∠D=60°,CD=8cm.求: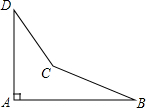 一个飞机零件的形状如图所示,按规定∠A应等于90°,∠B,∠D应分别是20°和30°,李师傅量得∠BCD=143°,就能断定这个零件不合格,你能说出其中的道理吗?
一个飞机零件的形状如图所示,按规定∠A应等于90°,∠B,∠D应分别是20°和30°,李师傅量得∠BCD=143°,就能断定这个零件不合格,你能说出其中的道理吗?