题目内容
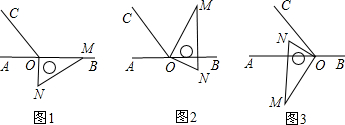
4.如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=112°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:直线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒4°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为多少?
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
分析 (1)延长NO到D,根据余角的性质得到∠MOB=∠MOC,等量代换得到∠COD=∠AOD,于是得到结论;
(2)分两种情况:ON的反向延长线平分∠AOC或射线ON平分∠AOC,分别根据角平分线的定义以及角的和差关系进行计算即可;
(3)根据∠MON=90°,∠AOC=68°,分别求得∠AOM=90°-∠AON,∠NOC=68°-∠AON,再根据∠AOM-∠NOC=(90°-∠AON)-(68°-∠AON)进行计算,即可得出∠AOM与∠NOC的数量关系.
解答 解:(1)平分,理由:延长NO到D,
∵∠MON=90°∴∠MOD=90° 
∴∠MOB+∠NOB=90°,
∠MOC+∠COD=90°,
∵∠MOB=∠MOC,
∴∠NOB=∠COD,
∵∠NOB=∠AOD,
∴∠COD=∠AOD,
∴直线NO平分∠AOC;
(2)分两种情况:
①如图2,∵∠BOC=112°
∴∠AOC=68°,
当直线ON恰好平分锐角∠AOC时,∠AOD=∠COD=34°,
∴∠BON=34°,∠BOM=56°,
即逆时针旋转的角度为56°,
由题意得,4t=56°
解得t=14(s);
②如图3,当NO平分∠AOC时,∠NOA=34°,
∴∠AOM=56°,
即逆时针旋转的角度为:180°+56°=236°,
由题意得,4t=236°,
解得t=59(s),
综上所述,t=14s或59s时,直线ON恰好平分锐角∠AOC;
(3)∠AOM-∠NOC=22°,
理由:∵∠AOM=90°-∠AON∠NOC=68°-∠AON,
∴∠AOM-∠NOC
=(90°-∠AON)-(68°-∠AON)
=22°.
点评 此题考查了角的计算,关键是应该认真审题并仔细观察图形,找到各个量之间的关系,是解题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
16.某城市对用户的自来水收费实行阶梯水价,收费标准如表所示:
(1)某用户5月份缴水费45元,则该用户5月份的用水量是多少?
(2)若某用户的月用水量为m吨,请用含m的代数式表示该用户月所缴水费.
| 月用水量 | 不超过12吨的部分 | 超过12吨不超过18吨的部分 | 超过18吨的部分 |
| 收费标准(元/吨) | 2.00 | 2.50 | 3.00 |
(2)若某用户的月用水量为m吨,请用含m的代数式表示该用户月所缴水费.
14.抛物线$y=-\frac{1}{2}{x^2}$不具有的性质是( )
| A. | 开口向下 | B. | 对称轴是y轴 | ||
| C. | 当x>0时,y随x的增大而减小 | D. | 函数有最小值 |
 如图,△ABC中,AB=AC,∠A=36°,请你利用尺规在AC边上求一点P,使∠PBC=36°(不写作法,保留作图痕迹)
如图,△ABC中,AB=AC,∠A=36°,请你利用尺规在AC边上求一点P,使∠PBC=36°(不写作法,保留作图痕迹)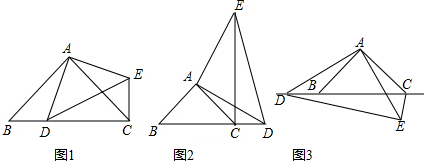
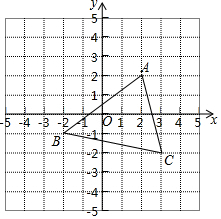 如图,每个小正方形的边长为1个单位
如图,每个小正方形的边长为1个单位