题目内容
12．已知代数式A=6x+4y-5，B=2（x+y）+（x-3）．（1）当x=y=-2时，求A-B的值；
（2）请问A-2B的值与x、y的取值是否有关，试说明理由．
分析 （1）根据整式的加减运算求出A-B=3x+2y-2，再将x=y=-2代入3x+2y-2中即可得出结论；
（2）根据整式的加减运算求出A-2B=1，由此即可得出A-2B的值与x、y的取值无关．
解答 解：（1）A-B=6x+4y-5-[2（x+y）+（x-3）]=6x+4y-5-（2x+2y+x-3）=6x+4y-5-2x-2y-x+3=3x+2y-2，
当x=y=-2时，A-B=3x+2y-2=3×（-2）+2×（-2）-2=-12；
（2）A-2B的值与x、y的取值无关，理由如下：
∵A-2B=6x+4y-5-4x-4y-2x+6=（6x-4x-2x）+（4y-4y）+（-5+6）=1，
∴A-2B的值与x、y的取值无关．
点评 本题考查了整式的加减运算，熟练掌握整式的加、减运算是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
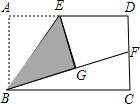（1）操作发现：如图，小明在矩形纸片ABCD的边AD上取中点E，将△ABE沿BE折叠后得到△GBE，且点G在矩形ABCD内部，将BG延长交DC于点F，认为GF=DF，你同意吗？说明理由．
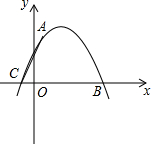如图，二次函数y=ax2+bx+c的图象经过点A（1，4）与B（5，0），C（-1，0）．
