题目内容
6.(-1,y1),(2,y2)与(3,y3)为二次函数y=-x2-4x+5图象上的三点,则y1,y2,y3的大小关系是( )| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y2<y1<y3 |
分析 把原函数解析式化简成顶点式,然后根据函数图象的性质即可比较大小.
解答 解:∵(-1,y1),(2,y2)与(3,y3)为二次函数y=-x2-4x+5图象上的三点,
∴把函数y=-x2-4x+5变形为:y=-(x+2)2+9,
∴由函数图象可知当x=2时此函数有最大值为9,当x>-2时,y的值随x的增大而减小,
∴y1>y2>y3,
故选:B.
点评 本题考查了二次函数的增减性.当二次项系数a>0时,在对称轴的左边,y随x的增大而减小,在对称轴的右边,y随x的增大而增大;a<0时,在对称轴的左边,y随x的增大而增大,在对称轴的右边,y随x的增大而减小.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
16.下列方程中有相等的实数根的是( )
| A. | x2+x+1=0 | B. | x2+8x+1=0 | C. | x2+x+2=0 | D. | x2-2x+1=0 |
14.将下列长度的三根木棒首尾顺次相接,能组成三角形的是( )
| A. | 1cm,2cm,3cm | B. | 2cm,2cm,4cm | C. | 3cm,4cm,12cm | D. | 4cm,5cm,6cm |
11.下列给出的条件中,能判断四边形ABCD是平行四边形的是( )
| A. | AB∥CD,AD=BC | B. | ∠B=∠C;∠A=∠D | C. | AB=AD,CB=CD | D. | AB=CD,AD=BC |
18.在-π,$\frac{1}{3}$,$\root{3}{4}$,0,$\sqrt{25}$,3.14,76.0123456…(小数部分由相继的正整数组成)中,无理数的个数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
15.化简|$\sqrt{2}$-1|+1的结果是( )
| A. | 2-$\sqrt{2}$ | B. | 2+$\sqrt{2}$ | C. | 2 | D. | $\sqrt{2}$ |
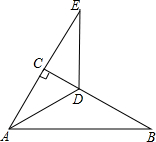 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.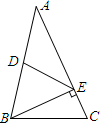 如图,在△ABC中,AB=AC,点D是AB的中点,BE⊥AC于点E.若DE=5cm,S△BEA=4S△BEC,则AE的长度是( )
如图,在△ABC中,AB=AC,点D是AB的中点,BE⊥AC于点E.若DE=5cm,S△BEA=4S△BEC,则AE的长度是( )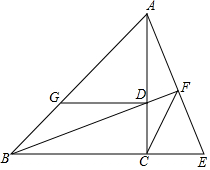 如图,在△ABC中,∠ACB=90°,∠ABC=45°,D为边AC的一动点(不与点A、C重合),过点D作DG∥BC,交AB于点G,AF⊥BD,AD交BD的延长线于点F,AF的延长线与BC的延长线交于点E.
如图,在△ABC中,∠ACB=90°,∠ABC=45°,D为边AC的一动点(不与点A、C重合),过点D作DG∥BC,交AB于点G,AF⊥BD,AD交BD的延长线于点F,AF的延长线与BC的延长线交于点E.