题目内容
16.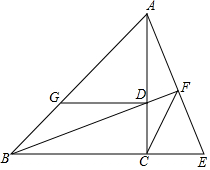 如图,在△ABC中,∠ACB=90°,∠ABC=45°,D为边AC的一动点(不与点A、C重合),过点D作DG∥BC,交AB于点G,AF⊥BD,AD交BD的延长线于点F,AF的延长线与BC的延长线交于点E.
如图,在△ABC中,∠ACB=90°,∠ABC=45°,D为边AC的一动点(不与点A、C重合),过点D作DG∥BC,交AB于点G,AF⊥BD,AD交BD的延长线于点F,AF的延长线与BC的延长线交于点E.(1)请写出与AD相等的线段,AD=DG;
(2)求证:DG+CE=BC;
(3)点D在边AC上移动时,∠BFC的大小是否发生变化?若变化,请求出它的变化范围;若不变,请求出它的度数.
分析 (1)先DG∥BC得出∠AGD=∠BAC=45°,即可得出结论;
(2)先用同角或等角的余角相等判断出∠CBD=∠CAE,进而得出,△BCD≌△ACE,即CD=CE最后用等量代换即可得出结论;
(3)先求出∠CED=45°,再由∠ACE=∠BFE=90°,得出点C,D,F,E四点共圆,用同弧所对的圆周角相等即可得出结论.
解答 解:(1)∵∠ACB=90°,∠ABC=45°,
∴AC=BC,
∵DG∥BC,
∴∠AGD=∠ABC=45°,
∴AD=DG,
故答案为DG;
(2)∵∠BCD=90°,
∴∠CBD+∠BDC=90°,
∵∠ADF=∠BDC,
∴∠CBD+∠ADF=90°,
∵AF⊥BD,
∴∠ADF+∠CAE=90°,
∴∠CBD=∠CAE,
在△BCD和△ACE中,$\left\{\begin{array}{l}{∠CBD=∠CAE}\\{BC=AC}\\{∠BCD=∠ACE=90°}\end{array}\right.$,
∴△BCD≌△ACE,
∴CD=CE,
由(1)知,DG=AD,
∴DG+CE=AD+CD=AC=BC;
(3)∠BFC的大小不发生变化,是45°,
理由:如图,连接DE,以DE为直径作圆.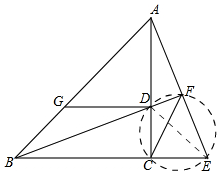
由(2)知,△BCD≌△ACE,
∴CD=CE,
∵∠DCE=90°,
∴∠CED=45°,
∵∠ACE=∠BFE=90°,
∴点C,D,F,E四点共圆,
∴∠DFC=∠CED=45°,
即:∠BFC=45°,是定值.
点评 此题是三角形综合题,主要考查了平行线的性质,三角形的内角和,全等三角形的判定和性质,四点共圆,解本题的关键是判断出△BCD≌△ACE.是一道比较简单的中考常考题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
6.(-1,y1),(2,y2)与(3,y3)为二次函数y=-x2-4x+5图象上的三点,则y1,y2,y3的大小关系是( )
| A. | y1<y2<y3 | B. | y3<y2<y1 | C. | y3<y1<y2 | D. | y2<y1<y3 |
11.若|x-2|+(x-y-1)2=0,则多项式-y-(x2+2y2)的值为( )
| A. | -7 | B. | 5 | C. | -5 | D. | -13 |
8.一元二次方程x2+2x-2=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
5.在数0,7,-81,(-9)2中,有平方根的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.在平面直角坐标系中.已知A(0,4).B(-2,0)在坐标轴上确定点P.使△AOP与△AOB相似.则符合条件的点P共有( )
| A. | 6个 | B. | 5个 | C. | 4个 | D. | 3个 |
 如图,在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$的图象与一次函数y=k(x-2)的图象交点为A(3,2)与B点.若C是y轴上的点,且满足△ABC的面积为10,则C点坐标为(0,1)或(0,-9).
如图,在平面直角坐标系xOy中,反比例函数y=$\frac{m}{x}$的图象与一次函数y=k(x-2)的图象交点为A(3,2)与B点.若C是y轴上的点,且满足△ABC的面积为10,则C点坐标为(0,1)或(0,-9).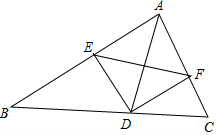 如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ADC的高,下列说法中正确的有( )个
如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ADC的高,下列说法中正确的有( )个